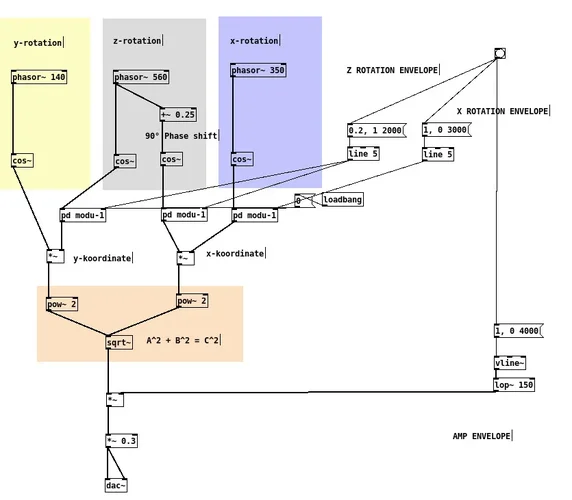
Soso, braucht man das? Für einen reellen Oszillator reicht doch ein komplexer Zahlenraum, der ja eine Ebene ist, 2D, und die Zeitachse verläuft orthogonal durch diese.
Oder besser gesagt: Sinus ist reell, Cosinus ist imaginär.
er ist gar nicht nur imaginär in dem sinne, denn man spricht an vielerlei stellen in der signalverarbeitung von
imaginären signalen, die aber äh... trotzdem tatsächlich existieren.
ich dachte bei dieser cosinus sache daher auch sofort an den komplexen sinus, der genau das ist, nämlich 2 signale.
wobei dort dann jedes der signale (die ja jeweils aus zeit vs. werte bestehen) als eine dimension gilt und man dann von einem zweidimensionalen oszillator spricht, der aus x = cos(Θ) und y = sin(Θ) besteht.
wobei die amplitude genau so fest vorgegeben ist wie der offset zwischen beiden und auch am verhältnis von periode und frequenz ist nicht zu rütteln - man kann das ganze dings mit einem einzigen wert beschreiben, z.b. "50".
Aber ich befürchte, deine Antworten findet wieder mal keinen Anschluss in meinem autodidaktisch-dilettantisch angeeigneten Halbverständnis. Bear with me.
mein möglicherweise bestehender einfluss akademischer sichtweisen und begriffliochkeiten muss nicht richtiger oder besser sein, aber er erleichtert die kommunikation ganz erheblich - auch für autodidakten und eklektiker, zu denen ich ja genau so gehöre wie du.
wenn so ein mathematiker richtig loslegt versteht man eh nix mehr. und was nützt mir auch zu wissen, was z.b. modulo eigentlich ist, wenn es doch eh in sämtlichen programmiersprachen "falsch" benutzt wird.
und da sich die akademiker ja auch permanent darum streiten wie irgendwas zu machen und zu nennen ist und wer nun recht hat, sollte man das alles nicht überbewerten.
nur die grundprinzipien sollte man beachten; wenn man die these aufstellt, dass es eine dritte dimension in einem elektrischen oder digitalen system gibt, sollte man das auch begründen können.