sospro
○□○□
Das wäre dann 4Dletztendlich kann man ja alles was man wollte als weitere Dimension bezeichnen .. man könnte einen Stereo-VCO haben bei dem man das Panning als 3. Dimension bezeichnet
Folge dem Video um zu sehen, wie unsere Website als Web-App auf dem Startbildschirm installiert werden kann.
Anmerkung: This feature may not be available in some browsers.
Das wäre dann 4Dletztendlich kann man ja alles was man wollte als weitere Dimension bezeichnen .. man könnte einen Stereo-VCO haben bei dem man das Panning als 3. Dimension bezeichnet
ich versuch das morgen zu erklären, mein Anspruch ist schon verstanden zu werden.
Was nicht verstanden wird ist schlecht oder falsch erklärt
Mechanisches Gyroskop, oder Kreiselstabilisator.
was ist die dritte Dimension?Das wäre dann 4D
..ich mach das mal motiviert "ähnlich" nach..hab da mal mit nem 3D Programm einfache Funktionen programmiert , dazu physics with Gravitation und Kollision isn Spiel gebracht
Anhang anzeigen 156103
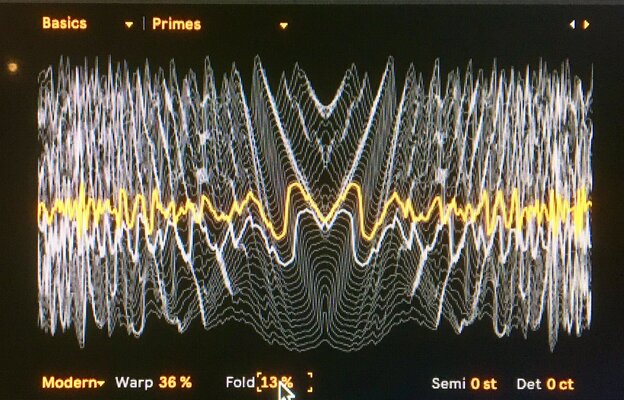
Ich finde die Idee recht interessant. Ich denke der 'Clue' wäre es interessante Anregungen für die 3D Rotationen zu finden.Die genaue Berechnung hier ist
x =(1 + ( cos( pi2 * ph3) -1 ) *zdep)* cos( pi2 * ph2) * r
y =(1 + (sin( pi2 * ph3) -1 ) *zdep)* sin( pi2 * ph) * r
z =(1 + ( sin( pi2 * ph2) -1 ) *zdep)* cos( pi2 * ph ) * r
wobei man z explizit im Moment gar nicht braucht,
mit ph = Phase und pi2 = 2 * Pi und zdep velocityabhängiger Wert,
r radius
und der Output ist sqrt( x*x + y*y) was dann noch mindestens einen DC Blocker braucht.
Ehrlich gesagt durchschaue ich selbst nicht 100% welche Modulation an welcher Stelle genau entsteht. Die Phasen selbst laufen linear durch, wobei man x auch noch per Feedback auf Phase 1 legen kann was dann wirklich FM ist, aber beim Output weiss ich nicht so genau was es ist.
Eben mooncast's mono 3D OSC, plus das Stereo Panning...was ist die dritte Dimension?
genau, ausserdem kennt man den Radius ja schonWarum nicht sqrt (x²+y²+z²)?
Vermutlich, weil das dann immer 1 ist?
genauAlso ist es nur die 2D-Projektion von einem sich bewegenden Punkt in dem 3d Gebilde?
kann man auch, hatte ich zuerst, dann wollte ich zwei Achsen mischenWarum wählst du als Output sqrt(x^2 +y^2) und nicht direkt den Output einer Achse? Dann hättest du kein DC Problem, wäre dann aber vermutlich reine AM.
wenn zdep == 1 dann sind es einfach die Dimensionen wie bisher beschrieben,Was bedeuted (geometrisch) der zdep Parameter? Für zdep=1 scheint es mir einfach eine Kombination aus Rotationen entlang der drei Raumachsen zu sein.
ja. Eine Änderung der Betrachtungsebene in Echtzeit sollte eigentlich kein Problem sein.
ja oder ähnlich eben.deine erklärung bezieht sich ausschließlich auf zuschreibungen, nicht auf das verfahren selbst.
die frage ob es das schon gibt bezog sich doch sicherlich auf das verfahren als solches.
Ich denke nur 2 Dimensionen, denn die Zeit und Phase sind doch quasi aequivalent, bzw. linear durch 2*pi verknüpft? Quasi die "Kreis-Zeit" oder "Zeit auf dem Kreis".Also eine Schwingung an sich ist ja schon mal was regelrecht 3-dimensionales. Erste Dimension ist die Zeit, zweite Dimension ist die Auslenkung (Amplitude), dritte Dimension ist die Phase, der Kreiswinkel in der Einheit rad(?). Die Sinus- oder Kosinusfunktion, das wurde hier im Thread irgendwo schon konstatiert, ist ja nur die Projektion einer kontinuierlichen ungedämpften Kreisbewegung auf zwei Dimensionen x und y. Kannst du, @mooncast, auf dieser Basis erklären, was bei deinem Oscillator neu ist? Einfache Modulation der Amplitude, der Kreisgeschwindigkeit ("Frequenz") kann es ja nicht sein, es sei denn, du willst uns alten Wein in neuen Schläuchen verkaufen. Oder zumindest unabsichtlich, weil du - wie ich übrigens - lieber programmierst als Fachliteratur zu wälzen. Let's both mind the trap of thinking it be new what we're doing.

Ich denke nur 2 Dimensionen, denn die Zeit und Phase sind doch quasi aequivalent, bzw. linear durch 2*pi verknüpft? Quasi die "Kreis-Zeit" oder "Zeit auf dem Kreis".
ich programmiere tatsächlich nur ungern und hab sicher 500 bis 1000 Papers zum Thema Audiosynthese zumindest überflogen.weil du - wie ich übrigens - lieber programmierst als Fachliteratur zu wälzen
tatsächlich must Du nur für Sinus entweder x oder z rotieren, aber so funktioniertsIch interpretier das mit den 3 Dimensionen so:

Wenn man nur x und y rotiert, dann hat man einen Sinus und wenn dann noch z dazukommt, wirds komplex (kann ich mir bildlich auch nicht mehr vorstellen)
könnte man, ja, sollte man vielleicht auch.Ansonsten kann man noch eine Koordinatentransformation durchführen, um aus 3 Achsen 2 zu erzeugen, z.B. Clarke-Transformatio
tatsächlich war es am Anfan eine Vektorotation über Matrizen die in Pixilang eingebaut ist,um die lästigen Sinus bzw. Cosinus Funktionen los zu werden.
Demnach wäre f(x) = nx+m also eine Schwingung, keine lineare Funktion. Man braucht schon die Phase, also eine Komponente, die periodisch durch ihren Ausgangspunkt in einer der anderen Dimensionen geht. -- Aber kann mich irren, SekII-GK-Mathematiker, Mathe war bei mir nicht mal Abi-Prüfungsfach.sicher, es sind nur 2, zeit und amplitude.
Demnach wäre f(x) = nx+m also eine Schwingung, keine lineare Funktion. Man braucht schon die Phase, also eine Komponente, die periodisch durch ihren Ausgangspunkt in einer der anderen Dimensionen geht. -- Aber kann mich irren, SekII-GK-Mathematiker, Mathe war bei mir nicht mal Abi-Prüfungsfach.
Nein. Dimensionen sind skalar.das sind dann auch alles dimensionen.
ja,Kann aber natürlich sein, dass ich mich damit ins Bockshorn jagen lasse,
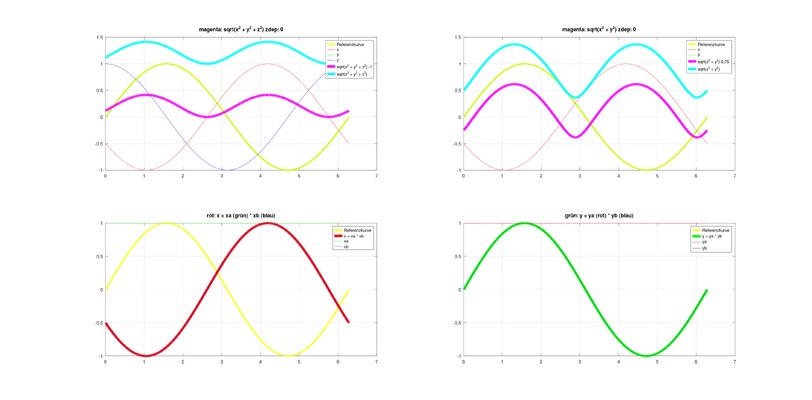
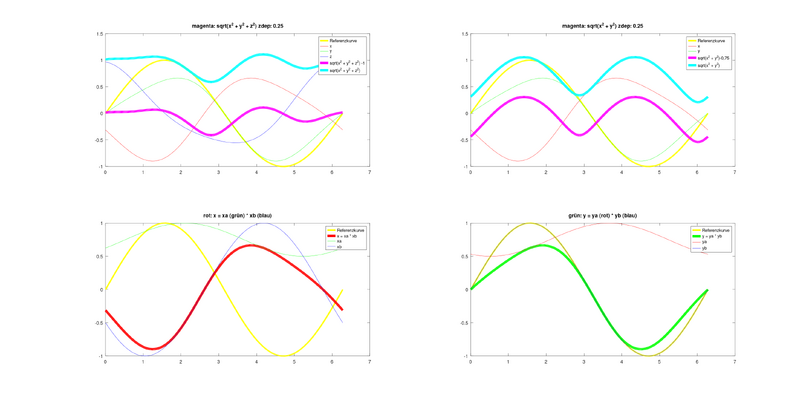
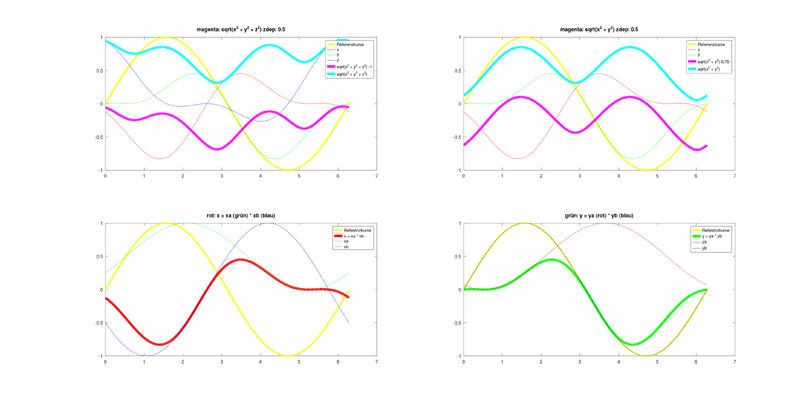
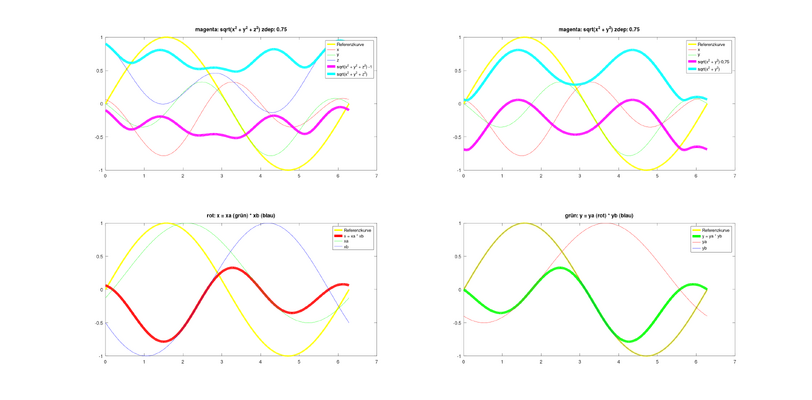
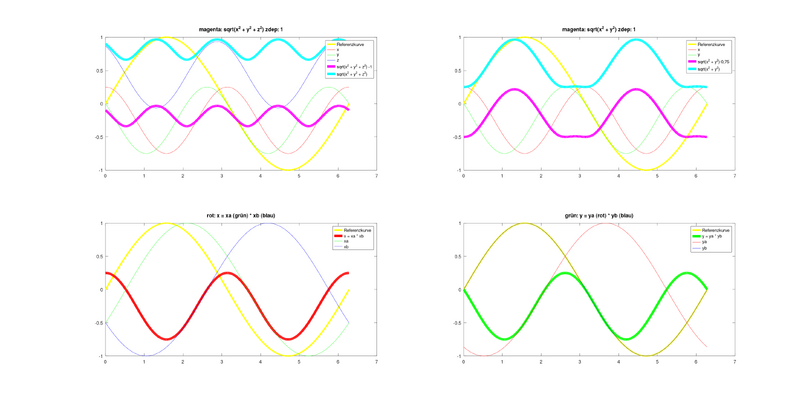

da hast du ein Missverständnis, weder der zdep Paramter noch der Offset haben hier etwas mit dem Peak zu tun.
Nein. Dimensionen sind skalar.
Aber ich merke, das wächst mir schon über den Dummkopf. Wenn ich doch mal Fachliteratur in die Hand nehme, wird da jedenfalls nicht nur mit sin() und cos() gerechnet
sondern gerne auch mit komplexen Zahlen.