Aloha .-)
Ist das denn jetzt der frei schwingende Stab (also Aufhängung mittig) oder ist der an einem der Enden befestigt ?
Was ist mit der Dicke? Ein dicker Stab ist steifer als ein dünner, also ist er bei gleicher Länge vom Ton her höher.
Jenzz
Der Stab ist an einem der Enden befestigt und zwar mit einer Flanschkupplung:

Diese Flanschkupplung hab ich auf ein Kantholz geschraubt und die Aufnahmeöffnung durchgebohrt, sodass der 1 m lange Messingstab da hindurchgeht. Den Bereich, der nicht mitschwingen soll hab' ich mit einem Frotté-Handtuch umwickelt, während der freie Teil mit dem Geigenbogen zum Schwingen angeregt wurde. Dabei hatte ich zuerst versucht, von der fast vollen 1m-Länge auszugehen und diese zum Schwingen zu bringen. Dabei zeigte sich aber, dass das mit dem Geigenbogen nicht ging. Die Grundschwingung war in diesem Längenbereich viel zu niedrig (geschätzt wenige Hz). Lediglich bestimmte
Obertöne ließen sich in Abhängigkeit von der Position der Erregung entlocken. Da ich aber die
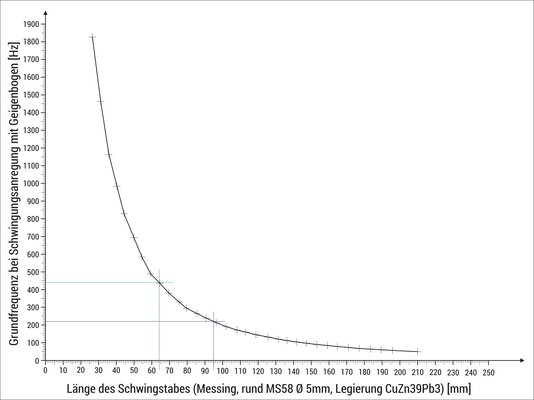
Grundschwingungsfrequenzen in Abhängigkeit der Länge messen wollte, hab' ich letztlich mit einem ca. 26mm aus der Flanschkupplung herausragenden Stummel begonnen und konnte nun tatsächlich die Grundschwingung anregen. Von da an habe ich Messwertepaare ermittelt, jeweils die Länge um ca. 5-6mm (aber genau gemessen) erhöht. Kurios fand ich auch die Tatsache, dass die jeweils gemessene Frequenz nicht absolut konstant ist, sondern vom Anpressdruck des Bogens und der Streichgeschwindigkeit abhängt*.
Das Ausgangsmaterial ist - wie in der Koordinatenbeschriftung zu lesen - 5mm dick. Da die 9 Stäbe auf meiner "Kalimbalimba" auf einem Hartholzsteg mittels besagter Flanschkupplungen senkrecht befestigt werden, werde ich wahrscheinlich als tiefste Frequenz 110 oder 220 (und nicht 440Hz) nehmen. Bei zu großer Länge resultiert auch über Hebelwirkung eine zu große Bruchgefahr für die Resonanzdecke. Die Anregbarkeit der Stäbe (mittels Bogen) ist ja auch ziemlich abhängig von deren Länge...
*PS: ein weiterer Parameter ist mir eingefallen: Die Bogenspannung! Bei zu wenig Spannung erfolgt überhaupt keine Schwingungsanregung, bei zu hoher wird sie schlechter und irgendwo dazwischen liegt ein Optimum; wahrscheinlich wieder kein linearer Zusammenhang, eher hyperbolisch...