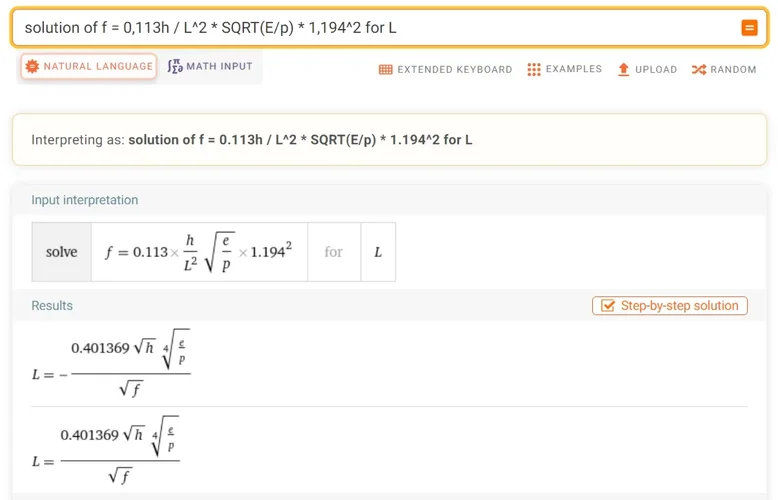
Die Formel für die Frequenz ist F~= 0.162 * (a/L^2)* SQRT(Y/d)
a* Dicke, L=Länge, Y= Youngs modulus, d= Dichte
Ich krame die Formel jetzt nochmal hervor, weil ich gerade dabei bin, meine "Kalimbalimba" zu bauen. Das Resonanzgehäuse ist soweit fertig, die Kalimbazungen schwingen auch wunderbar und zwar mit kräftiger Resonanz aus dem Gehäuse (richtig schön viel Sustain...), aber:
Die "Nagelgeigen"-Einheit, die ich auf das Gehäuse montieren will muss noch dimensioniert werden. Und zwar habe ich einen Hartholzsteg gefertigt, der 9 Bohrungen mit 5mm Durchmesser zur Aufnahme der schwingenden Stäbe bekommen hat. Die Stäbe werden mittels Flanschmuffen auf dem Steg befestigt und können mittels Rändelschrauben so justiert werden, dass beim Feintuning jeder Stab auch einige Zentimeter in das Gehäuse hineingeschoben werden kann.
Als Material habe ich Messingrundstäbe (5mm) vom gängigen Typ CuZn39Pb3 vorgesehen. Die 9 Stäbe sollen nach Art einer "Keltic-Moll" Tonleiter gestimmt werden. In folgender Tabelle sind die entsprechenden Frequenzen markiert:
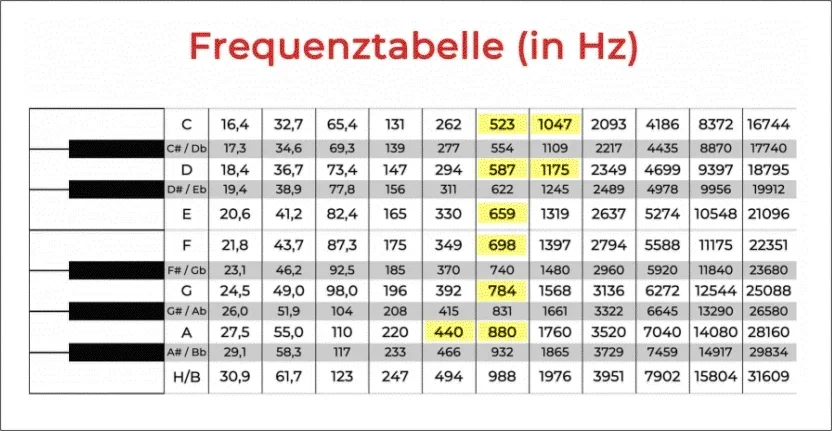
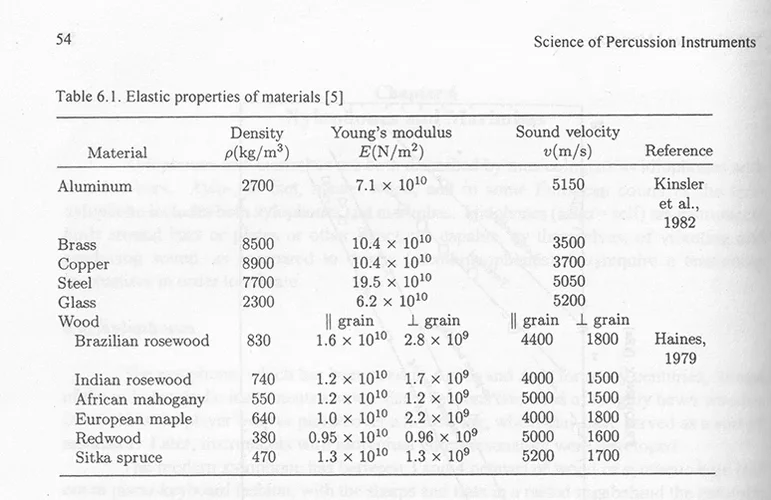
Als Parameter für besagtes Messing habe ich noch gefunden:
Young's Modulus (=Elastizitätsmodul) : 97 [GPascal]
Dichte : 8,47 [g/cm^3]
Kannst Du mit Deiner Formel daraus die erforderlichen Stablängen errechnen?
Irgendwie kommen bei mir da unplausible Werte bei heraus. Die ominöse "Konstante" 0,162 scheint auch nur für Stäbe mit quadratischem Querschnitt zu gelten. Mein physikalisches Kurspraktikum für Mediziner und Pharmazeuten reicht leider nicht aus, da komplett durchzusteigen...

PS:
Falls alle Stricke reißen, geh' ich ganz pragmatisch vor und bestelle mir zwei 1m-Stücke, spanne eines davon in die Muffe bei definierter Länge (z.B. 980mm) und messe mittels App die Grundfrequenz. Da sich Länge und Frequenz ja zueinander umgekehrt proportional verhalten (ich hoffe auf einen linearen Zusammenhang...) müsste ich anhand dieser Messung ja eigentlich alle erforderlichen Längen für obige Frequenzen errechnen können, oder?