Synthesizer-Diplom

Synthesizer Diplom ist ein Pamphlet, welches ich Mitte der 90er schrieb, um digitale Synthesizer näher zu beleuchten als Arbeit bei der Schule für Tontechnik aka SfT in Wuppertal (Audio Engineer / Audio Producer). http://www.sequencer.de/synthaudio/synthesizer-diplom.html

Auch als PDF http://www.sequencer.de/pix/synthaudio_pics/synthdiplom.pdf (ohne Bilder leider). Im Folgenden auch ohne Bilder.. Bau ich evtl später dazu..

SYNTHESIZER - DIPLOM

von --- Moogulator.com - 13:44, 14 August 2007 (CEST) Uhrheberrechtlich geschützt, bitte bei Ausschnitten fragen.. nicht einfach kopieren (C) 1996/97 by Consequence Mic Irmer (Moogulator) kontakt / adresse / email moogulator

0 Vorgeschichte des Synthesizers

Synthesizer History Milestones/Vorgeschichte und Geschichtliche Meilensteine

• Synthesizer Vorgeschichte
• Synthesizer History Timeline

Hauptteil

2. Digitale Grundlagen / global

2.1 Was ist "digital"?

Bevor die Vorteile und die Technik von "Analog"- und "Digital" Synthesizern besprochen werden, ist es nötig, den Unterschied zu erklären: "digitale" Zustände kommen in der Natur nicht vor, es ist eine Technik der Vereinfachung durch Darstellung von physikalischen Größen in einem Zahlenraster. Konkret: eine Steuerspannung, die jeden Wert annehmen kann, ist formgleich; wie in der Natur; eine analoge wert- und zeitkontinuierliche Größe. Wenn man diese Größe als digital bezeichnen will, so bedeutet dies, sie wird als Zahlenwert auf einer ebenfalls gerasterten Zeitachse als diskrete Zahl ausgedrückt (Beispiel für die: y Achse: Auflösung: 8 Bit = 65536 Werte, dadurch ergeben sich Stufungen; erhöht man die Auflösung, werden die Stufen kleiner, aber niemals so fein wie das analoge "Soll-Pendant"; die x Achse: wieviele "Proben" werden genommen pro Sekunde?). Um das digitale Signal dem Analogvorbild anzunähern, kann man:

- Die Anzahl (Auflösung) der Werte zwischen Maximal- und Minimalpunkt vergrößern (die Treppe hat mehr Stufen = feineres Abbild). Ein Analogwert ist stufenlos, der digitale muß hier zwischen zwei diskreten Werten unterscheiden (="Quantisierung") und kann nur innerhalb dieser Werte operieren.

- Mehr Werte auf der x-Achse entsprechen häufigerem "Abfragen", also mehr Einzelproben, die "Samples" (Treppe hat schmalere Stufen = feineres Abbild). Häufigeres Abfragen erhöht die oberste hörbare, wiedergegebene Frequenz, muß also nicht "gegen unendlich" tendieren, wie der y-Wert, sondern kann im hörbaren Bereich bleiben. Hierbei sind noch andere Dinge wichtig, welche mit der Abtastung zusammenhängen. Zu nennen sei hier das "Nyquist-Theorem", das ähnlich dem Effekt des scheinbaren Rückwärtslaufes von Filmen besagt, die doppelte Abtastfrequenz zu verwenden, um nicht ungewollt Wellendurchläufe zu "überspringen" und somit falsch wiederzugeben. Dies soll zugunsten des Umfangs der Arbeit nicht weiter vertieft werden.

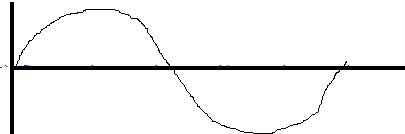
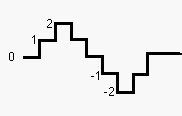
unperfekte Zeichnung:

Als Beispiel für die Reduktion einer analogen auf eine digitale Wellenform hier eine Prinzipskizze (Seite 6 oben) einer Sinuswellenform. Die Umwandlung ist nötig, um sie mit Computern weiterverarbeiten zu können.

Ein letzter Punkt zur Verdeutlichung ist die praktische Umsetzung in die Realität: Ein Analogsynthesizer ist aus verschiedenen Baugruppen (also Modulen), welche eine bestimmte Funktion erfüllen, zusammengesetzt. Jede Baugruppe kann, wie bei analogen Modularsystemen gut zu erkennen, als eine in sich geschlossene, (fast) autarke Einheit gesehen werden, die mit anderen Modulen durch entsprechendes Patchen verbunden werden. Bei nicht- oder teilmodularen Systemen sind diese Verbindungen bereits ab Werk intern verdrahtet. Ein reiner Digitalsynthesizer besteht ebenfalls aus solchen Baugruppen mit dem Unterschied, daß sie als Computerprogramme (bzw. "Unterprogramme") in Form eines Algorithmus bestehen. Diese (Einzel-)algorithmen besitzen die Möglichkeit zur Übergabe von Parametern zur Ein- und Ausgabe, welche mit den Patchkabeln zwischen den Analogmodulen vergleichbar sind.

Jetzt kann man erkennen, daß der Digitalsynthesizer eine Datenverarbeitungsanlage, ein Computer, ist. Dieser ist, weil er ja keine (analogen) elektrischen Spannungen oder verschiedene Schalldrucke verarbeitet, sondern mit Algorithmen (also Zahlen) umgeht, mit Wandlern ausgestattet sein, die das digitale "Signal", also Zahlenkolonnen, in elektrische Spannungen (Spannungsschwankungen) umsetzen (und umgekehrt).

Die Vorteile der digitalen Geräte sind:-

leichter / preiswerter herstellbar- reproduzierbare Ergebnisse / mögliche Verarbeitung durch Computer- neue Funktionen leichter integrierbar / austauschbar

2.2 Sampling

Ein "Sample" ist die digitale Aufnahme eines Geräusches, welches oft als Erweiterung subtraktiver Synthesizer eingesetzt wird (siehe Kapitel "Synthesetechniken"), um Naturklänge oder Startphasen eines Klanges (sehr entscheidend zur Erkennung eines Instrumentes) authentischer und schneller zur Verfügung zu haben.

Um Samples zu benutzen, müssen diese im Speicher des Synthesizers (also des Computers im Synthesizer) abgelegt sein, welche entweder ab Werk fest in einem Chip (einem ROM = Read Only Memory, siehe dazu Abschnitt 2.3 Computer) oder von außerhalb in den Daten-Speicher des Synthesizers geladen werden. Dies geschieht durch Datentransfer über eine Schnittstelle oder Massenspeicher wie Disketten oder Festplatten. Eine übliche Methode ist die Benutzung von Analog- / Digital (A/D) - Wandlern, welche die Entsprechung bei der Ausgabe durch Digital / Analog (D/A) - Wandler sind. Hierbei gibt es viele Methoden. Die zur Zeit übliche ist die "Delta Sigma" Wandlung (Messung relativ zum vorangegangenen Meßwert).

Wie Tonhöhenänderungen erreicht werden siehe auch Kapitel 3.2.1.

Samples haben einen Start- und Endpunkt, sowie eine (oder mehrere) Schleifenbildungmöglichkeit(en) mit eigenen Start- und Endpunkten ("Loopstart- und Endmarkierung"). Die Schleife(n) sind für die Phase des Klanges, in der die Taste gedrückt bleibt, zuständig. So ist es möglich, auch einen Streicherklang "unendlich langzuziehen", bis die Taste losgelassen wird (durch Wiederholen, also "Loopen" eines Teils des Samples). Der Ausklang kann auch oft mit einer zweiten solchen Schleife ("Loop") belegt werden.

Professionelle und aktuellere Sampler haben zumeist eine komplette subtraktive Einheit mit "an Bord" und sind somit auch als Synthesizer zu sehen (wie zum Beispiel der E-mu "Emulator IV"). Die Oszillatoren haben hier Samples als "Wellenform", die nachher eine Filtereinheit passieren, das heißt: dynamisches Verändern bestimmter harmonischer Teiltöne. Natürlich können auch die Grundwellenformen als Sample benutzt werden, digitale Oszillatoren sind oft ebenfalls in dieser Weise realisiert (andernfalls werden sie algorithmisch, also nach einer Rechenvorschrift in einem Programm erzeugt). Deshalb kann man "Sampler" und "Synthesizer" nicht getrennt sehen, wie auch der "Workstation"-Begriff (Synthesizer mit eingebautem Sequencer und Schlagzeugsounds) lediglich auf eine Spezialisierung hinweist, und die Grenzen zunehmend verschwimmen oder gar nicht mehr zu erkennen sind.

Eine Auswahl einiger digitaler Synthesizer und Samplermodule: Von oben nach unten (rechtes Foto): - Ensoniq ASR - 10 (Sampler mit Effektprozessor) & Wechselplattenlaufwerk - Yamaha TG-77 (FM-Synthesizer mit Samplewiedergabe = "AFM") - ( YAMAHA Effektprozessor SPX 900 ) - Waldorf Microwave (Hybrid Wavetable-Synthesizer) - Clavia Nord Lead (digitaler virtueller "analog"-Synthesizer) - EMU Emulator IV (Z-Plane-Sampler)& Wechselplattenlaufwerk (nicht im Bild) ( Ensoniq Effektprozessor DP/4 )

Fotos sind hier leider nicht mehr, aber alle Synthesizer befinden sich in der Synthesizerdatenbank! SynthDB

Von oben n. unten (Linkes Foto): Oberheim Xpander(Analog-Synthesizer) Korg Prophecy (M.O.S.S. Synthesizer) Ensoniq SQ80 (Hybridsynthesizer)

2.3. Computer

2.3.1 Hardware

Ein Computer ist eine Einrichtung zur Eingabe, Verarbeitung und Ausgabe von Daten. Im Prinzip werden nur Kombinationen von "Einsen" und "Nullen", genauer gesagt zwei Zuständen, wie z.B. "5 Volt" oder "0 Volt", benutzt. Diese Zustände werden im Binär- (oder Dual-) System dargestellt, ein Zahlensystem mit der Basis zwei. Proportional zum dezimalen (Zehner-) System können die Stellen der Ziffern durch eine Potenz dieser Basiszahl dargestellt werden:

2343 (dezimal)= 2x 103 + 3x 102 + 4x 101 + 3x 100

Ein zweites Beispiel: 1001 (binär)= 1x 23 + 0x 22 + 0x 21 + 1x 20 Der Dezimalwert dieser Binärzahl entspricht dem Ergebnis der Potenzen (hier also "9").

Die einzelnen Ziffern zeigen auch deutlich, daß der maximale Wert durch Hinzunahme einer weiteren Ziffer verdoppelt werden kann. Die Bitbreite (Datenwort), die ein Computer gleichzeitig verarbeiten kann beträgt meist 8,16 oder 32 (usw...). Obwohl ein Byte = 8 Bit sind, ist es unüblich, die Prozessorwortbreite in Byte anzugeben. Nun aber erst einmal zur technischen Seite, um die Fremdworte zu erklären: Das obige zweite Beispiel ist eine 4-Bit Zahl. Will man die Gesamtspeicherkapazität angeben, so kann man die üblichen Bezeichnungen der Physik verwenden, also "1 KiloByte" für 1000 x 1 Byte = 1024 Byte, abgekürzt "1 kB". Die 1024 ergeben sich durch 8 Bit, die 1 Byte enthält.

Zentrales Element des Rechners ist die CPU (Central Processing Unit = Prozessor), welche(r) aus Rechenwerk, Steuerwerk und einem kleinen Speicher (="Register") besteht. Diese CPU ist über Busse / Bussysteme (=parallele Leitungen, die die Information, jene oben beschriebenen Binärinformationen, weiterleiten) mit dem eigentlichen Arbeits- und Datenspeicher (RAM und ROM, siehe unten,) sowie der Ein- / Ausgabe verbunden, z.B: Tastatur, Display oder Wandler (eine Einrichtung zum Umsetzen von analogen in digitale Signale und umgekehrt). Ein Taktsignal bringt den Prozessor dazu, den nächsten Schritt, einen Befehl, auszuführen. Genauer: den Befehlszähler "weiterzuschalten", bzw. Zwischenschritte zur Lösung mathematisch - logischer Probleme "weiterzuschalten".

Hier die wichtigsten Bestandteile und Bezeichnungen eines (rudimentären) Computers:

Befehl: Eine Anweisung an das Rechenwerk oder den Befehlszähler, eine logische Operation durchzuführen, z.B.: Springen (bedingt oder unbedingt), addieren, o.ä. (...)

Betriebssystem: Programm, das die Grundfunktionen des Systems enthält (wird vom Anwender nicht geändert), jedoch die Benutzeroberfläche, die "Schnittstelle" zwischen Mensch und Gerät (Bekannte Betriebssysteme sind u.a.: "Mac OS", "Windows ´95" oder "OS/2" bei Computern).

Bus: Eine Reihe von parallelen Leitungen zur Übertragung der binären Information: Adressbus: Wählt eine Speicherzelle oder einen Speicher der Ein- / Ausgabe an (Synthesizer: Der Wandler soll einen Wert auslesen oder hineinschreiben oder: Displayausgabe anwählen, usw...). Datenbus: Ein Wert wird hier ein- / ausgegeben (z.B: Ausgabe des Wertes an das Display: Es soll "Attack=12" anzeigen). Steuerbus: Synchronisation aller Rechnerkomponenten und Organisation.

EPROMS / EEPROMS: "Festspeicher" - ROMs, die löschbar und beschreibbar sind. Das doppelte "E" (für "electrical eraseable") deutet auf die generell elektrisch mehrmalige Lösch- und Beschreibbarkeit hin. Dieses Bauteil wird oft verwendet für die Parameterspeicherung der Einzelklangprogramme, die einfacheren EPROMs hingegen werden gern für das Betriebssystem genutzt, da es nicht sehr oft ausgetauscht werden muß ("Eraseable Programable ROM" = begrenzt häufig löschbares ROM). Diese Speicher werden nicht durch Ausschalten gelöscht.

Hardware: Die Technik, ("festverdrahtet").

Programm: Eine logische Folge von Befehlen (Arbeitsanweisungen), welche aus einem festbegrenzten und für diesen Prozessor (CPU) genormten Vorrat von Befehlen aus einer Gesamtvorratsliste besteht.

Rechenwerk: Der Prozessor-Teil, in dem (z.B.) addiert wird, also der Befehl ausgeführt wird, wie etwa: "Eine Zahl aus dem Daten - Speicher holen, zu einer anderen hinzuaddieren und das Ergebnis in einer weiteren Speicherzelle ablegen".

Schnittstellen / IO-Ports: Verbindungen mit anderen Geräten über genormte, physikalische "Hardwarekommunikationsverbindungen" und Softwareprotokolle zur Steuerung der Datenübergabe. Hierüber werden andere Geräte angeschlossen, wie Drucker oder Synthesizer (über MIDI = Musical Instrument Digital Interface = Normschnittstelle für Musikinstrumente). "IO-Ports" steht für "Input - Output - Anschluß", also Ein- / Ausgabebausteine, bzw. Schnittstelle(n).

Software: Programme und Daten, ("veränderbar").

Speicher: Der Speicher ist eine Einrichtung aus einzelnen "Speicherzellen", die durch den Adressbus angewählt werden. In einer solchen "Speicherzelle" ist eine Zahl gespeichert, die auch wieder über den Datenbus ausgelesen, gelöscht oder überschrieben werden kann. Dabei gibt es das RAM (Random Access Memory = Speicher mit freiem Zugriff) als Arbeits- und Datenspeicher, aus dem Daten ausgelesen und geschrieben werden können und das ROM (Read Only Memory = Nur - Lese - Speicher), aus dem nur gelesen werden kann. Hier stehen für den Anwender unveränderliche Daten. In Synthesizern sind das u.a.: Tastatursteuerung, (Werks-) Sampleklänge / (Werks-) Sounds (=Parameter dieser Klänge). Es gibt auch die Möglichkeit, das Betriebssystem in ein RAM zu laden und bei jedem Neustart (über Diskette / Festplatte) jedesmal erneut alle Daten zu laden. Meist ist das Betriebssystem von Synthesizern jedoch im ROM zu finden. RAMs werden gelöscht beim Ausschalten, (E/EP)ROMs nicht. ROMs behalten ihren Inhalt ebenfalls. Eine Akkupufferung der RAMs ist eine Möglichkeit, um dieses Problem zu umgehen.

Steuerwerk: Koordiniert den Ablauf des Programms. Es weist das Rechenwerk an, einen Befehl umzusetzen und das Ergebnis in den prozessorinternen Zwischenspeicher zu bringen, bzw. in / aus dem Speicher (RAM / ROM) zu lesen, wo Daten (etc...) gelesen oder gespeichert werden sollen.

Die Aufgaben sind:

1.Adressierung (Anfahren einer bestimmten Speicherzelle) 2.Auslesen 3.Decodierung (Heraussuchen des Befehls aus der "Vorratsliste" / Anweisung des Rechenwerkes) 4.Ausführung eines Befehls eines Programms anzuweisen.

Noch einige Worte zu logischen Verknüpfungen und Operationen: Jede der verschiedenen Befehle für das Rechenwerk (alle mathematischen Operationen, jedoch nicht die "unbedingten Sprungbefehle") werden durch ihre Kodierung ausgewählt, z.B.: Befehl "011" kann bedeuten: "addieren" oder: "durch eine UND Logikoperation verknüpfen".. Sprungbefehle werden zwar auch in dieser Art kodiert, führen aber nur zur Änderung des Befehlszählerstandes.

Hier exemplarisch die Arbeitsweise des logischen "UND": Die Wertetabelle für das logische UND lautet:

Bei Variable 1 Variable 2 Ergebnis 0 0 0 0 1 0 1 0 0 1 1 1

Nur wenn Variable 1 UND Variable 2 = 1 sind, ist das Ergebnis 1. Solch eine Wertetabelle wird aufgestellt und dann in Form einer Schaltung realisiert, auch bei anderen logischen Verknüpfungen.

Beim logischen ODER wäre dies also:

Bei Variable 1 Variable 2 Ergebnis 0 0 0 0 1 1 1 0 1 1 1 1

Wenn Variable 1 ODER Variable 2 gleich 1 ist, ist das Ergebnis 1.

Man kann der besseren Anschauung wegen auch "wahr" und "falsch" benutzen (statt "0" und "1") oder auch "offene" und "geschlossene" Schalter, etc.. Bei Benutzung von Schaltern ist die Reihenschaltung zweier oder mehrerer Schalter mit der UND Schaltung identisch, die Parallelschaltung hingegen entspricht dem logischen ODER.

Interessant ist, als letztes Beispiel, der Addierer für binäre Zahlen, stellvertretend für andere Funktionen hier beschrieben:

Wenn Ziffer1 und Ziffer2 binär addiert werden, gibt es nur diese Möglichkeiten:

0+0=0 ; 0+1=1, bzw. 1+0=1 ; 1+1=1.

Zusätzlich muß für die nächst höherwertige Stelle ein "Übertrag" gesetzt werden ("Übertrag =1"). Wenn kein Übertrag mehr gesetzt wird, ist somit das maximal errechenbare Ergebnis erreicht, bzw. begrenzt durch die Stellenanzahl! Das "Additionsergebnis" ist ein logisches "ODER" -Verhalten. Der Übertrag ist ein logisches "UND" (beides natürlich Verknüpfungen zwischen den beiden Ziffern als Variable).

Nun erkennt man die Realisierbarkeit aus logischen Funktionen von mathematischen Problemen! Die Gesamtheit der mathematischen Befehle sind in einem Arithmetik- und Logik - Netzwerk im Rechenwerk enthalten. Des weiteren enthält es "Register" als Zwischenspeicher (1 Byte groß). Auf dieser Ebene rechnet der Computer jeden einzelnen Befehl (jede Zahl nacheinander) aus.

Es können in neueren Prozessoren theoretisch auch parallel Zahlen addiert werden, dies beschleunigt den Rechner dadurch, daß er innerhalb eines Prozessor - Taktschritts mehrere Zahlen bereits addiert hat. Die Wortbreite des Prozessors muß natürlich entsprechend groß sein.

Ein aktuelles Beispiel für die Anwendung des parallelen Ausnutzens des gesamten Prozessorbusses (etc...) ist "MMX" für Intel Pentium- Prozessoren.

2.3.2 Software

Als Befehlstypen für die Software gibt es für den einfachsten Rechner somit: Transferbefehle (Speicher- und Registerinhalte vertauschen oder mit einem Wert "laden"), Sprungbefehle und Rechenoperationen sowie organisatorische Befehle (z.B: Stop).

Wie sieht dies nun praktisch aus? Es wird eine Software (ein Programm) geschrieben, welches alle logischen Schritte zu einer Problemlösung enthält und nacheinander abarbeitet: Die Summe dieser Einzeloperationen führen dann zum Ziel, wie z.B: Die Errechnung einer Sinuswelle, die Filterung oder das Lauter- und Leiserwerden durch eine "Hüllkurve" gesteuert, die in Echtzeit berechnet werden muß, d.h. sie ist nun "nur" ein Programm, bzw. ein Programmteil! Es gibt hier Sprünge und Unterprogramme, die eine bestimmte Aufgabe haben..

Ein fiktiver Computer soll eine positivflankige Dreieckswellenform ausgeben, beherrscht aber nur die Befehle "addieren", "subtrahieren", "springen" und "Transferbefehle", die durch den Prozessor vorgegeben sind. Dies könnte so aussehen:

Die komplette Befehlsliste wäre hier zunächst zu definieren (durch den Hersteller bereits getan). - Alle möglichen Aufgaben, die der Prozessor (CPU) beherrscht, sind die folgenden:

Befehlsnummer: Befehl: (Maschinenbefehl) 000 Setze (Wertzuweisung einer variablen Speicherzelle des Prozessors = Register) 001 Addiere x (Addition eines Wertes zum jetzigen Registerwert) 010 Subtrahiere x (Subtraktion vom aktuellen Registerinhalt) 011 Springe nach x, wenn reg (Sprung zu einer anderen Befehlszeile im Programm Befehlszähler=x, wenn Bedingung erfüllt). 100 Springe nach x, wenn reg=0 (dito) 101 Gehe zu x (unbedingter Sprung zu einer Befehlszeile (Befehlszähler=x). 110 Transferiere Register nach Adresse y (der Registerwert wird in eine andere Speicherzelle/Ausgabe geschrieben).

Die Synthax (eine formale Regel der Befehlsstruktur) ist hierbei:

(Befehlsform:=) Befehl (was soll getan werden?), Variable (wo sind die Daten?)

Ein Programm zu obigem fiktivem Problem lautet:

Maschinenbefehl Befehlszähler: Befehl: 000,0 0 Setze reg = 0. 110,adr 1 Transferiere Registerinhalt nach "Ausgabeadresse". 001,1 2 Addiere zum Registerinhalt 1 hinzu (reg=reg+1). 011,max 3 Ist reg < maxmum? Dann springe nach Programmnummer 1. 110,adr 4 Tranferiere Registerinhalt an Ausgabeadresse. 010,1 5 Subtrahiere von Registerinhalt 1 (reg=reg-1). 100,0 6 Ist reg=0 ? Dann springe nach Programmnummer 4. 101,1 7 Gehe zu Programmnummer 1 (zurückspringen nach oben / auf Befehlsnummer 1 springen, also Befehlszähler auf 1 setzen).

adr=Ausgabeadresse; max=Maximaler möglicher Wert; reg=variables Prozessor-Speicherregister (der sogenannte "Akkumulator")

Diese Maschine braucht 3 Bit zur Kodierung aller Befehle. Eine weitere Bitfolge, welche durch die Breite des Busses begrenzt ist, ist für den eigentlichen Wert, z.B: bei 8 Bit Wortbreite gibt es 65536 Zustände (Die Zahlen 0 bis 65535); kleinere Stufungen als zwischen den Ziffern (also Kommastellen) sind nicht möglich.

Der Wandler kann diese Wertefolge sooft pro Sekunde ausgeben (und halten), daß ihre Frequenz von der Geschwindigkeit des Rechners abhängig ist (taktabhängig). Dieses Beispiel müßte daraufhin optimiert werden, auf ein Signal der Tastatur mit der richtigen Frequenz der Dreieckwelle zu reagieren, denn das Programm gibt in dieser Version nur ein steigendes, dann fallendes "Signal" aus, was natürlich nicht sehr realitätsnah ist. Wenn nun eine Modulation zu dieser Frequenz noch hinzukommt (aufmoduliert werden soll), muß dieses Programm abermals eine Änderung erfahren; gemäß des Standes des Pitchwheels ("Tonhöhenbeugungsrad") muß dann sein Wert "aufaddiert / subtrahiert" werden. In der Praxis werden andere Verfahren benutzt, dazu später mehr..

Das Programm arbeitet so, daß es zunächst einen Wert definiert (Null) und ihn danach, durch Zuzählen von "Eins", steigen läßt und dies wiederholt, bis der Maximalwert erreicht wurde. Dann verläßt es die bedingte Schleife (Befehle 1 bis 3), und danach wird immer wieder "Eins" subrahiert, bis "Null" erreicht wird. Die nächste bedingte Schleife (Befehle 4 bis 6) wird dann beendet. Hernach wird ein Sprung zu dem Punkt initiiert, nachdem der Wert zum ersten Mal auf "Null" gesetzt wurde, was eine Endlosschleife darstellt. Der Transferbefehl steht für das "nach außen bringen" des errechneten Wertes, ohne den das Programm sinnlos wäre.

Anhand dieses sehr einfachen Programms kann man nun sicher jeden logischen, einfachen Einzelschritt leicht nachvollziehen, und es wird für die Realisation eines Synthesizers wesentlich klarer, wie so etwas generell programmiert werden kann. Wichtig ist vor Allem das Wissen, daß es sich nur um die Gesamtheit vieler ineinander verschachtelter Programmteile handeln kann (und muß). Die einzelnen Operationen sind sehr einfach.

Die Befehlsstrukur eines modernen und leistungsstarken Power - PC - Chips, wie er beispielsweise in einem Apple Macintosh Computer verwendet wird, erreicht um die einhundert verschiedene Befehle, es kommt nur auf die sinnvolle, gut strukurierte und geplante Programmierung mit einfachen Befehlen an, die die "Intelligenz" der Software ausmacht! Die "Intel"-Prozessoren arbeiten nach einem anderen Prinzip, nämlich mehr Befehle zu beherrschen, dafür aber mehr Taktzyklen zu benötigen - es gilt auch hier: aus "ein wenig mehr" Befehlen das Programm logisch zu strukturieren, etc... Welche Prozessorstrukur verwendet wird, ist prinzipiell völlig irrelevant, und außerdem erleichtern Programmiersprachen diese Arbeit und sind für alle Rechner erhältlich (zur Zeit meist "C++"). Diese arbeiten auch mit Befehlen, welche schon eine Kette der (oben erklärten) Maschinen-Befehle beinhalten und danach übersetzt ("compiled") werden in die computereigene Maschinensprache (auch "Maschinencode" oder "Mnomics" genannt). Innerhalb dieser Sprache sind selbstverständlich auch Schleifen (etc...) möglich, sowie die Bildung einer Bibliothek aus Programmen, welche oft verwendet werden, wie etwa die Eingabe, Fourieranalyseberechnungen, Bildschirmausgabe, Zeichnen eines Kreises, usw...

Nun zu der tatsächlich verwendeten Methode der digitalen Oszillatoren, welche eine bestimmte Wellenform ausgeben können. Eine Methode ist das Auslesen einer Liste ("table - lookup"-Verfahren) von Werten aus dem ROM, welche die Wellenform (keiner bestimmten Frequenz) beschreibt, eine Kurvenform, wie z.B. eine Sinuswellenform. Die Auslesegeschwindigkeit für einen Durchlauf - Zyklus (Eine komplette "Wellenberg- und Talfahrt" = eine Periode) ist bestimmend für die jetzt hörbare Frequenz, die auch von anderen Quellen leichter modulierbar (beeinflußbar) ist. Denn auch hier gilt: Ein Durchlauf pro Sekunde entspricht einem Hertz. Ein Vielfaches durchlaufen ergibt die entsprechende Wunschfrequenz. Die Anzahl der Werte in dieser Tabelle ist allerdings auch begrenzt und wird durch Weglassen oder Interpolieren (s.u.) angeglichen, um alle Tonhöhen zu erreichen. Dieses Verfahren ist verhältnismäßig wenig rechenintensiv, da die Werte schon direkt zur Verfügung stehen und nur "angepaßt" werden.

Die zweite Möglichkeit, die mehr "Echtzeitberechnung" erfordert, ist die algorithmische Generation der Werte, also ein rein mathematisches Erzeugen dieser Wellenform, was selbstverständlich nicht mit "Natur-Samples" funktioniert. Aber Möglichkeiten wie "Pulsbreitenmodulation" (dies ist das Verändern, bzw. Verschieben der Symmetrie einer Rechteckwelle) oder jede andere mathematisch beschreibbare "Wellenformänderungsart" sind ohne große Samplespeicher realisierbar, solange der Computer noch "Rechenpower" übrig hat. Des weiteren ist bei der Verwendung von Samples (eine sehr gebräuchliche Methode in aktuellen Geräten), ähnlich dem obigen Verfahren, die veränderte Auslesegeschwindigkeit ("sample rate") der gespeicherten Samples zur endgültigen Frequenzsteuerung eine potentielle Variation, die ältere Sampler verwendeten. Auch Kombinationen aus beiden Verfahren gibt es. Die Software kann bei allen Verfahren um neue Basiswellenformen, sogar "Wellenformverläufen", erweitert werden und ist prinzipiell jederzeit erweiterbar... Die bei höherer Ausleserate "fehlenden" Werte werden durch die sogenannte "Interpolation" berechnet. Interpolation bedeutet hierbei zwischen dem aktuellen und dem nächsten Wert einen "Mittelwert" zu bilden. Wichtig ist das nahtlose Übergleiten in einen anderen (den nächsten) Wert. Die benutzen Verfahren sind verschieden. Im obigen Verfahren benutzt man es zur Ergänzung fehlender Werte anhand gespeicherter Werte.

Eine andere Anwendung dieses Prinzips an ganz anderer Stelle soll hier kurz erwähnt werden: Der Clavia "Nord Lead" kann zwei Sounds ineinander überblenden, indem deren aktuelle Parametereinstellung gleichförmig in den "zweiten Parametersatz" übergeleitet werden: Während ein Parameter "Cutoff" des Werte - Bereichs 0-127 von "45" auf "122" gebracht werden muß, kann ein anderer Parameter "Waveform OSC1" des Werte - Bereichs 0-2, also "Dreieck", "Sägezahn" oder "Rechteckwelle" von "1" auf "2", also von "Sägezahn" auf "Rechteck", gebracht werden und dies in entsprechendem Verhältnis in derselben Zeit. Diesen Weg empfindet man als "morphing", denn es ist keine Überblendung im Sinne einfacher Lautstärkebalanceregelungen, daher ist der Begriff "Überblenden" hier und im weiteren Verlauf nicht wörtlich zu nehmen. Bekannt ist diese Technik auch im Grafikbereich.

Einen Eindruck dieser Überblendungsberechnung kann man auch grafisch aus der Wellentabelle des Microwave bekommen (Abbildung in Kapitel 3.2.1).

(BILD NICHT HIER, ABER IN DER synthDB: Aufgeräumt: Der CLAVIA Nord Lead mit "parametermorphing" von innen (2 DSPs unter mittleren Platine). Links: DSP und Prozessor (quadratisch), sowie Software-EPROMS (etikettiert).

2.3.3 Modulation (Performance - Probleme mit digitaler Technik)

Auch wenn das Synchronisationsproblem des fiktiven Beispielcomputerprogramms gelöst ist, z.B. durch zeitsynchrone Programme, interne Uhr etc..., gibt es nun die Aufgabenstellung der begrenzten Taktgeschwindigkeit und damit auch eine begrenzte Arbeitsgeschwindigkeit. Dies ist die Rechenleisung, genannt "performance". Das bedeutet auch: Ein superschnelles "Algorithmus-LFO" (s.u.), eine "Hüllkurve" etc.., also viele zeitaufwendige Modulationen brauchen mehr Performance und müssen begrenzt werden durch diese Maßnahmen:

A. Eine begrenzte Anzahl der modulierenden Quellen.

sowie

B. EineGeschwindigkeits und Auflösungsbegrenzung der Modulatoren (Beispielsweise: LFOs = Niederfrequente Oszillatoren, die maximal auf 30 Hz beschränkt sind). Oftmals auch in Form der "Updatezeit" des Systems.

Diese Anforderungen werden sicher durch die Wünsche der späteren Käufer gesetzt, und danach richtet sich auch die Leistung der Hardwarezusammenstellung (Prozessor, Taktfrequenz etc..) und dessen Geschwindigkeit / Effizienz.

Ein praktisches Beispiel: Die Firma Waldorf muß zur Erstellung des "Microwave 2" einige Überlegungen anstellen, um "Performance zu sparen": Man ist entschlossen, zwei LFOs mit einer maximalen Frequenz von 100 Hz, 10 Stimmen, 2 Multimodefilter (24 dB und 6 dB) usw... zu realisieren. Dazu nimmt man im Vergleich zum Vorgänger "Microwave" nicht nur eine neue Hardware (zwangsweise mit höherem Takt und (oder) schnellerem Prozessor), sondern spart Dinge ein, wie MIDI Filter pro Multimodesound (um MIDI-Controller oder Programmwechselbefehle jeweils einzeln pro Sound auszufiltern) oder Modulationsverbindungen etc.. Dadurch ergibt sich: Da diese Funktionen selten alle gefordert wurden, bekam die Hardware "etwas Rechenzeit zurück", die für mehr Stimmen oder Filtermöglichkeiten oder auch die neue "Ringmodulation" (Erklärung: s.u.) frei nutzbar ist. Die Frage, was nun erreicht wird, (oder was evtl. weggelassen werden kann) ist Firmenpolitik oder eine Finanzfrage... Zumindest sind theoretisch keine Grenzen -außer der Rechner Performance- gesetzt, jeder Funktion mehr oder weniger Möglichkeiten einzuräumen. Auch "nur" durch eine andere, verbesserte Software, die im Fall "Waldorf Microwave 2" von außen nachträglich änderbar ist, kann das System total umfunktioniert werden. Hiermit werden Optionen möglich wie etwa ein Angebot, eine Funktion, welche der Käufer gerne implementiert hätte, zu verbessern oder erstmals zu integrieren. Sehr deutlich wurde dies durch ein Gespräch mit dem Waldorf-Spezialisten mit etwa dem Fazit: "Wenn ich herausbekomme, wie die Softsynchronisation funktioniert, liefern wir sie im nächsten Update sofort nach". Oft kann ein Programm noch optimiert und eventuelle Fehler beseitigt werden. Als Beispiel sei schließlich das Update (=neue Softwareaktualisierung) des Clavia "Nord Lead" erwähnt, welcher mit derselben Hardware nun mehr Filtertypen, einige Drumsets ("elektronische Schlagzeugsounds") und diverse andere Verbesserungen bekam, denn auch für den Hersteller ist es von Vorteil, ein stets aktuelles Gerät auf dem Markt zu haben. Dem schon erwähnten Microwave 2 gab man daher auch die Möglichkeit mit, ihm über die MIDI-Schnittstelle ein neues Betriebssystem zu senden, welches sich dann praktisch auf einer Diskette für gängige Sequencer-Programme -wie Steinbergs "Cubase"- leicht verwirklichen läßt. Es ist schließlich auch möglich, dieserart Daten über eine Mailbox oder das Internet zu beziehen...

Um ein anderes System zu nennen und nocheinmal zu verdeutlichen, wie offen und flexibel die Konstruktionen selbst sein können: Die Quasimidi "Rave-O-lution 309" ist ebenfalls ein Computersystem, welches prinzipiell auch andere Funktionen übernehmen könnte. Dieses Gehäuse und diese Bedienelementeform hat man dem Gerät "mitgegeben", um mit einer Spezialisierung auf Drums und Bass, sowie der Livetauglichkeit und spontanen Änderungsmöglichkeit der Parameter entsprechend gerecht zu werden und diese perfekt meistern kann. Eine Softwareänderung (in z.B. einen "FM Synthesizer") wäre hier natürlich wenig sinnvoll und mit einem "500´er Mercedes" zu vergleichen, der jetzt zu einem Transporter umgebaut werden soll, nur weil er die gleiche Motorleistung hat. Ein letztes Beispiel sind offene Computersysteme wie Symbolic Sounds "Kyma". Die Synthesestruktur ist völlig frei definierbar, und man kann sich hier sein "digitales Modularsystem" selbst konfigurieren und parametrisieren: Es ist alles eine Softwarefrage und vor allem eine Rechengeschwindigkeitsfrage, wie flexibel der neue "virtuelle Synthesizer" jetzt ist, denn man hat nicht die Limits durch ein spezielles Gehäuse. Selbst der vielseitige Korg "Prophecy" kommt hier kaum mit..

(Bilder in der synthDB, nicht hier (sorry) Oben: Die Innenansicht des WALDORF Microwave. Rechts: Prozessor und Software-EPROMs. Unten: Yamaha TG77 FM-Synthesizer mit Samples (offen).

3. Synthesetechniken / speziell

3.1 Subtraktive Synthese / Sampling

Grundlagen und wie digitale Filter funktionieren

3.1.1 Baugruppen

Die digitalen Komponenten der subtraktiven Synthese sind mit der gleichen Zielsetzung der entsprechenden Analogbausteine konstruiert worden: Ein oder mehrere Oszillator/en, die klangerzeugenden Teile des Systems, welche meist ein obertonreiches Spektrum besitzen, durchlaufen ein Filter, das einen Teil dieser Obertöne dynamisch -durch Herausfiltern bestimmter Teiltöne- verändert. Der klassische Aufbau besagt die Zusammenmischung der Oszillatoren vor dem Filter in einer Mischstufe, was auch heute die Regel ist. Nachgeschaltet ist ein Vertärker, der dynamisch kontrolliert wird und eine Panoramaeinheit, die die Verteilung zwischen linker und rechter Seite reguliert. So hat man die drei Blöcke aus der Analogwelt auch hier: Oszillatorteil für Tonerzeugung und Tonhöhe, Filterteil für Klang (beziehungsweise Obertonänderungen) und Verstärker- mit Panoramamodulteil für die Lautstärkenkontrolle. Der dynamische Verlauf dieser "Teile" ist dabei der wichtige Faktor. Modulation heißt, eine Steuerung eines Parameters eines Moduls oder Baugruppe durch einen anderen beliebigen oder "festverdrahteten" Parameter, der auch auf einem anderen Modul erzeugt worden sein kann (auch extern durch Schnittstellen.. u.a.).

Die wichtigsten Grundbausteine zur Steuerung der Hauptbauteile aus digitaler Sichtweise:

Hüllkurven ("Envelope"): Eine Liste von Pegeln, die in einer bestimmten, zugehörigen Zeit erreicht werden. Je nach Pegelstand wird ein Steuerwert dementsprechend übergeben (an den zu modulierenden Parameter). Alle resultierenden Zwischenstände sind durch Interpolation immer vorhanden. Einfachere Formen verwenden die gebräuchlichste Struktur "ADSR" (Attack, Decay, Sustain, Release), der Analogsysteme: Nach einer Zeit "Attack" wird das Steuersignal von Null- auf Maximalpegel gebracht, danach (innerhalb der Zeit "Decay") erfolgt der Rückfall auf den "Sustain"-Pegel. Die "Release"-Zeit gibt anschließend die Zeit an, die bis zum Erreichen des Nullpegels vergeht (in der Regel nach Loslassen der Klaviaturtaste). Selbstverständlich gibt es hier noch einige andere Arten, die aber demselben Zweck dienen: Mit Hüllkurven können (Steuerungs-) Verläufe automatisiert werden. Für den Lautstärke- und Filterteil steht meist standardmäßig je eine Hüllkurve zur Verfügung, sie werden dann durch (Klaviatur-) Tastendruck aktiviert ("getriggert") und gestartet.

LFOs: Im Gegensatz zu den normalen Audiooszillatoren (Schwingungsgeneratoren), schwingen diese "Low Frequency Oscillator", also "niederfrequente Oszillatoren" genannten Modulationsquellen im unteren Frequenzbereich mit regelbarer Frequenz. Dies würde weniger Rechenleistung als ein dementsprechender (im Hörbereich arbeitender) Oszillator benötigen. Der abgedeckte Frequenzbereich ist etwa zwischen 0,2 bis 30 Hz festgelegt, kann aber auch bei einigen Geräten wesentlich erweitert worden sein und in den Audiobereich hineingehen oder ihn ganz abdecken (für "FM-Synthese" notwendig, s.u.)! Auch hier sind verschiedene Wellenformen im Angebot. Eine immer häufiger in Instrumenten anzutreffende "Minihüllkurve" kann den LFO-Pegel ein- und ausblenden. Etwas wie z.B. "einschwingendes" und "abklingendes" Vibrato läßt sich so einfach simulieren.

Tracking: Dient der Anpassung von Klaviatur (Keyboard) und Controllern (MIDI-Pegellieferanten, die zur Echtzeitmodulation herangezogen werden) und gibt an, wie stark sich ein Parameter durch einen anderen verändern soll und wie (in welchem Verhältnis) er sich ändert, wenn sich der ursprüngliche Parameter ändert ("Skalierung"). Häufig verwendet ist das "Keytracking", je höher die gespielte Note (o.a. Parameter) auf der Klaviatur ist, desto mehr soll ein Filter öffnen oder bestimmte Hüllkurvenparameter verändert werden, welche dann Filter und Lautstärke steuern; für Pianoklänge ist dies dringend nötig! Andere Verwendungsformen sind: Anschlagstärkekennlinien, Klaviaturskalierungen, etc...

Für die Oszillatorensektion gibt es ebenfalls vielfältige Oberton-Variationsmöglichkeiten wie:-

Synchronisation eines Oszillators mit einem anderen, also das Erzwingen eines erneuten Wellenformstartes des synchronisierten Oszillators, gesteuert durch den Wellenverlauf (Periodendauer) des ersten (meist bei Nulldurchgang mit steigender Tendenz).- Waveshaping: Änderung der Wellensymmetrie oder Verformung der Welle nach bestimmten Gesetzen (wie digitale Übersteuerung "clipping"...etc...) - Frequenzmodulation (FM): In digitalen Geräten oft durch die Möglichkeit gegeben, durch einen Audiooszillator die Frequenz des nächsten zu modulieren. Hier können "metallische" und "glockige" Klänge leicht realisiert werden. Entscheidend ist das Verhältnis der Frequenzen.- Amplitudenmodulation (AM): dito, jedoch wird die Lautstärke des nächsten Oszillators gesteuert.- Phasensteuerung- / Modulation: Die Startphase / Phasenlage eines (mehrerer) Oszillators/en kann hier gesteuert werden, (z.B. durch den jeweils anderen Oszillator.)- Die Oszillatoren haben eine Technik der kontinuierlichen Wellenformveränderung durch mathematische Funktionen oder Wellenformtabellen- Die Oszillatoren geben Samples wieder, also gespeicherte "Aufnahmen" von Klängen.- Ringmodulation: Errechnet aus den Eingangsfrequenzen zweier Oszillatoren Summe und Differenz (aus "200Hz" und "150Hz" werden "350Hz" und "50Hz"). Diese resultierenden Frequenzen sind keine Vielfachen der Eingangsfrequenzen, da sie "unharmonische" Klänge erzeugen sollen. Diese Einrichtung kann auch als AM benutzt werden (Zweiter Oszillator ist frequenzmäßig unterhalb des Hörbereichs).

Die Filter sektion ist ein vielgeschätzter Teil und ein erst in letzterer Zeit klanglich ernstnehmbar und konkurrenzfähig zu analogen Pendants gewordenen Hauptbestandteile, denn es gilt nicht nur, einfach die folgenden Typen zu generieren, sondern auch die typischen Verzerrungen, Resonanzen und Rückkopplungen der analogen Vorbilder zu simulieren und zu verbessern. Dabei ist das Filter auch der eigentliche "Synthesen-Namensgeber", denn er sorgt für das "Subtrahieren", das "Abziehen" der Teiltöne im Frequenz-Spektrum (Amplituden aufgetragen zu den ganzzahligen x-fachen der Grundfrequenz). Eine Kurzerklärung der synthesizertypischen Filterarten folgt auf der nächsten Seite... (Rechts daneben findet man eine vereinfachte und stilisierte Prinzip Skizze mit "Resonanzbuckel" im LPF & HPF. Sie zeigt den Obertongehalt im Frequenzverlauf).

• LPF: Low Pass Filter (Tiefpaß): Sperrt ab einer

Eckfrequenz mit einer bestimmten Steilheit und filter lpf Resonanz (Erhöhung um die Eckfrequenz herum).

• HPF: High Pass Filter (Hochpaß): dito, allerdings

hpf sperrt er unterhalb der Eckfrequenz...

• BRF: Band Reject Filter ("Notch" / Kerbfilter):

notch Sperrt von einer unteren Frequenz bis zu einer oberen Frequenz (Bandbreite) mit einer Flankensteilheit (x dB/Oktave).

entspricht etwa umgekehrtem BRF

• BPF: Band Pass Filter (Bandpaß): Entspricht einer

Kombination aus LPF und HPF, dem "Gegenteil" von BRF: Läßt den Bereich zwischen zwei Frequenzen unter Berücksichtigung der Flankensteilheit durch.

Alle Filtertypen können einen "Resonanzbuckel" bekommen, der den typisch "elektronischen" Klang ausmacht. Diese sind Vertärkungen/ Betonungen um die Eckfrequenz herum. Die Resonanz ist bei guten Filtermodellen bis zur Selbstoszillation bringbar, und der kritische Punkt bei Vergleichen ist der Bereich "kurz vor Selbstoszillation", denn hier sind mathematische Verfahren der "chaotischen" Verzerrungssimulation rechenintensiv und schwierig zu programmieren / algorithmisieren (d.h. "zu mathematisieren"). Ein zweiter Punkt ist, wie stark die Resonanz den Klang "ausdünnt" (Gegenmaßnahme: "Rückkopplung" auf den Eingang / Ausgangsparameter beeinflussen aktuelle Berechnung).

Auch digitale vollparametrische Equalizer oder ganz spezielle Filterdesigns wie in E-mu´s Z-Plane - "Synthese" (oder besser Filterprinzip!!) sind willkommene Klangdesign-Alternativen; machbar durch die Kombination verschiedener Filtertypen, die parallel oder seriell verschaltet werden.

Die Steilheit der Filter wird durch Anzahl der "Pole" erkennbar (pro Pol: 6 dB pro Oktave Dämpfung). Die gebräuchlichste ist: 4 Pol LPF, also ein 24 dB/Oktave - Tiefpaß-Filter. Die E-mu Filtermodelle haben 14-polige Kombinationen aus obigen Filtertypen, wodurch auch "Kammfilter" (mehrere regelmäßige "Kerben") und Überblendungen zwischen Filterarten ("Filtermorphing") etc.. möglich werden. Die sogenannten APF (Allpaßfilter) kommen seltener zum Einsatz, sie haben keine "Filterwirkung", aber eine Phasenveränderung zur Folge, wie alle anderen Typen ebenfalls, was zusätzlich die oben erwähnte Errechnung erschweren kann.

Für Aufgaben mit Rechnungen wie obige sind digitale Signal Prozessoren (DSP´s) sehr gut geeignet. In Clavias "Nord Lead" ist ein DSP (aus der meistverwendeten "56000er-Familie", hier ein 56002 FC40) für jeweils vier Stimmen zuständig. Zusammen mit einem Motorola microwaveMC68331(CFC16), einem Hauptprozessor mit der ungefähren Leistung eines Atari Falcon oder eines älteren Apple "68K Macintosh" - Modells hat der Nord Lead mit drei DSPs zwölf Stimmen zur Verfügung. Der benötigte Platz für diese Hardware ist zudem äußerst gering! Wie im nächsten Kapitel näher erläutert, benutzt der Waldorf "Microwave 2" eine sehr ähnliche Hardware!

Bilder: http://www.sequencer.de/synthaudio/synthesizer_digital_filter.html

3.2.1 Wavetable-Synthese (Wavescanning / Wavesequencing)

(zB in ppg wave und waldorf wave, microwave 1 und 2 und waldorf microwwave xt und xtk)

Die im "Wave", dem "Microwave" und dem "Microwave 2" der Firma Waldorf verwendete Synthese soll hier nun näher -und stellvertretend für viele andere- exemplarisch beschrieben werden. Auch liegt es nahe, diese Geräte näher zu beleuchten, da es sich (neben Quasimidi) um eine der wenigen deutschen Synthesizer-Herstellerfirmen handelt. Dabei wird der volldigitale Microwave 2 den Hybridsystemen Wave und Microwave gegenübergestellt, die allesamt als Digitalsynthesizer in der Geschichte bereits länger verzeichnet sind: Anfangs noch von Wolfgang Palms Firma "PPG" aus Deutschland entwickelt (Wavecomputer 360/340, Wave 2 - 2.3 & Waveterm; Erscheinungsjahre:1978, ´81-´84) und schließlich von Waldorf aufgegriffen und erweitert, gipfelt in dem zur Zeit aktuellen Microwave 2, der nach Veröffentlichung dieser Arbeit herauskommen wird (ca. März ´97). "Hybrid" ist eine Mischform aus Digital- und Analogtechnik: Die (zwei) Oszillatoren sowie die komplette Wavetablesynthese- Technik ist dabei schon digital ausgeführt, auch Hüllkurven und LFOs.. Das Signal gelangt über eine Mischeinheit in eine analoge Filtersektion, im Microwave ein 24 dB/Okt. LPF (Tiefpaßfilter), der durch Chips der Firma Curtis gebildet wird. Danach folgt die Vertärkersektion und die Panoramaeinheit (Stereobalance-Modul = Panning), in welcher die gewünschte Stereoposition nach dynamischer Lautstärkebearbeitung eingestellt/moduliert wird. Die Filtereinheit ist beim Wave um einen resonanzlosen "12dB Hochpaß" erweitert worden, sowie um einige digitale und analoge Zusätze bereichert (zusätzliche Hüllkurve, Analogeingänge, etc...). Der Microwave 2 ist hingegen "ganz und gar" digital und besitzt zwei digitale Multimodefilter: Mit 24dB/Okt. als HPF/LPF oder 12dB/Okt. Flankensteilheit auch als BPF verwendbar. "Filter 2" hat lediglich 6dB/Okt., aber auch die Wahlmöglichkeit zwischen HPF und LPF und "festere Verdrahtung" (weniger Modulation!), im Gegensatz zu Filter 1. Wichtig zu wissen ist: Die digitalen Filter klingen natürlich nicht identisch mit den analogen Curtisfiltern im "alten" Microwave, da, wie schon erwähnt, Verzerrungen "chaotisch" und anders "mathematisiert" werden müssen (was in Analogtechnik unnötig ist, sondern einfach schon "da" ist)! Es gibt aber heutzutage keine Argumentationsmöglichkeit mehr, daß "digital" auch "schlechter" sein muß, es wird nur schlicht etwas "anders" klingen (aufgrund der völlig anderen Konstruktion)! 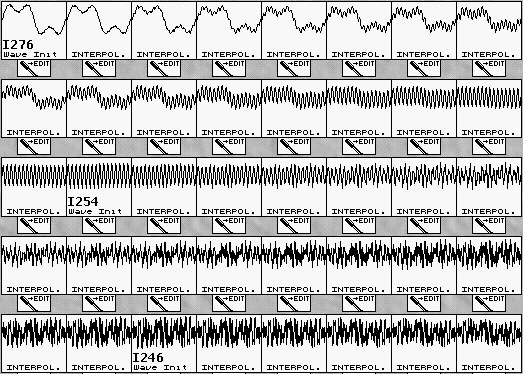Die Oszillatoren können, wie in subtraktiven Synthesizern, auch moduliert und in ihrer Tönhöhe justiert werden. Die entscheidende Andersartigkeit gegenüber subtraktiven Geräten ist das "Wavescanning" oder auch "Wavetable" (Wellensatztabelle) genannte Verfahren: Ein Wavetable ist eine Sammlung von 64 Wellenformen ("Waves"), welche wiederum aus 128 wählbaren Wellenformdatenschritten, hier "Samples" genannt, bestehen. Die einzelnen Waves sind tatsächlich jeweils ein "Durchlaufzyklus" (Periode) einer vollständigen Welle, welche in einem Computer verändert (editiert) werden können. Die drei Wellenformen Triangle (Dreieck), Square (Rechteck) und Saw (Sägezahn) sind in manchen Geräten in dieser Reihenfolge als Wellen 61 - 63 generell immer anwählbar, wobei die gewählte Wavetable die restlichen Waves liefert (beim Wave sind diese Waves 61-63 frei definierbar). Dies ist lediglich eine Festlegung des Herstellers und könnte softwaremäßig auch im Microwave geändert werden. Die wirkliche Synthese ist nun dergestalt, daß ein achtstufiger Hüllkurvengenerator ("Wave-Envelope", welche 8 Zeiten und 8 Pegel hat, die nacheinander angefahren werden) diese Wellentabelle "durchfährt". Sie schaltet also bei entsprechendem aktuellem Steuerwert der Hüllkurve die dazugehörige Wave proportional zum Steuerwert um und erzeugt den nichtstatischen Klang. Da auch längere Hüllkurven-Zeiten möglich sind, kann so auch ein längerer Verlauf mit unterschiedlichen Wellenformen durchfahren werden. Da ein einfaches Umschalten äußerst "ruckelig" klingen würde, treten hier die "Samples", die den Waves "untergeordnet" sind, ein, denn sie bilden eine echtzeitberechnete, interpolierte "Brücke" zwischen den einzelnen Waves und sorgen somit für ein weiches Überblenden. Ein Parameter "Wave Mode" kann von stepped ("stufig") auf smooth ("weich") geschaltet werden. Dies sorgt dafür, die "Samples" (Wellenperiodendaten einer Wave) zwischen den Waves über den "Computerzwischenspeicher" möglichst gleichformig (entsprechend der o.a. Einstellung) "überlaufen" zu lassen. Werden weniger Waves in ein Wavetable gesetzt (per Computer editierbar) können hier, durch mehr Platz für die Zwischenstufen, weichere Übergänge erzeugt werden, denn die fehlenden Waves werden durch Interpolation (ohne Speicherverlust) errechnet und "virtuell" an den freien Platz gesetzt. Die Hüllkurve besitzt durch ihre Achtstufigkeit eine große Bandbreite der Variation einer "Wellenfahrt" und die Möglichkeit, eine Schleife (Loop) zwischen zwei beliebige Stufen zu setzen. Die Modulation aller Zeiten gemeinsam und zusätzlich aller Pegel gemeinsam ist ebenfalls möglich. Ein noch größeres Potential ergibt sich durch die Tatsache, daß alle Parameter der Waldorf - Geräte mindestens ein- bis zweimal beliebig moduliert werden können, so auch die Wavetablefahrt!! Der zweite Oszillator muß sich zwar derselben Wavetable bedienen, kann jedoch frei darin "herumfahren" und andersartig moduliert werden. Ein zweiter Aspekt ist die freie Wahl des "Startsample", also der Phasenlage der Wellenperiode. Wenn diese auf "free" steht, wird eine zufällige Phasenlage gewählt. Mindestens 32 Wavetables gibt es. Dazu sind einige benutzerdefinierbar (z.B.: 12 Stück im Microwave). Die Auflösung der Wavetable-Technik ist 8 Bit, also 256 mögliche Schritte, auf der Auslenkungs-/(y-)Achse. Um andere Töne zu erreichen, wird die Ausleserate verändert und interpoliert (Werte weggelassen bei niedrigen, hinzugefügt bei hohen Tönen!). Diese ist von ca.160kHz auf ca.44kHz geändert worden, denn das 8fache Oversampling wurde hier verwendet (eine Technik im Zusammenhang mit Wandlern zur "Verbesserung" - Hier muß ich auf die Fachliteratur verweisen). Dies ist auch beim Sampling der Grund, warum Töne, die im Original auf "A" liegen, eine Oktave tiefer schon "verfremdet" wiedergegeben werden, da die Ausleserate dabei reduziert ist, für darüberliegende Oktaven aber zu viele Werte fehlen, um der höheren Ausleserate genügend Werte zu "liefern". Die Waldorfgeräte haben den sogenannten "Micky-Maus-Effekt" nicht (im Gegensatz zu Samplern), da hier genügend Werte errechnet (interpoliert) werden, die Samplern nicht zur Verfügung stehen und sogar die "Interpolationsqualität" eingestellt werden kann. Oft wird auch die Auslesegeschwindigkeit in Samplern nicht geändert (nur Interpolation). Doch zurück zum System: Da beim Microwave 2 nicht nur eine gespiegelte Halbwelle benutzt wird (64 Bytes), sondern eine ganze (128 Bytes), ein Relikt aus einer Zeit, in der Speicher noch sehr teuer waren, gibt es eine Verbesserung für viele Sounds (z.B. Pulsbreitenmodulation!). Hieraus ist auch die "Sample" Länge von 128 zu erklären. Ein weiteres klangerweiterndes Mittel kann die Mischstufe sein. Diese hat eine 3 Bit Auflösung; also kann von 0 bis 7 geregelt werden. Auch ein Noisesignal (Rauschgenerator) läßt sich hier zuregeln (ebenfalls von 0-7). Dies alles ist beim Microwave 2 höher aufgelöst (128 Stufen) und erlaubt bessere Ein- und Ausblendung der drei Klangquellen. Die Besonderheit der Mischeinheit ist nicht nur die Modulierbarkeit, sondern daß sich ab der Summe der beiden Oszillatorenlautstärken von "8" eine Verzerrung einsetzen läßt (Beim Microwave 2 ist dieser Wert entsprechend höher). Dies alles wird mit einem Motorola 8 Mhz - 68000 Prozessor erzeugt, der etwa die Leistung eines Atari ST hat -der Microwave 2 wird mit einem 68331 und einem DSP 56303 bestückt und läuft mit 21 Mhz, was erheblich schneller ist, und zudem dieses Prozessorderivat auch Wandler enthält (kosten- / platzsparend). Auch die zwei LFOs und die zwei Hüllkurven, sowie die achtstufige Wave-Envelope wird durch den Prozessor generiert. Der LFO 1 hat noch eine "Minihüllkurve", die es ermöglicht, diesen ein- ("Attack") und auszublenden ("Decay") und vorher noch zu verzögern ("Delay"). Die Symmetrie ist einstellbar. Dies ist das Verhältnis von "Wellenberg" ("positiver" Teil) zu "Wellental" ("negativer" Teil) in einer Periode. Die Humanizefunktion bringt einen von 0-7 einstellbaren Zufälligkeitseinfluß auf die LFO-Geschwindigkeit mit ein, welche ebenfalls regelbar ist und im typischen LFO - Bereich "bis ca. 25Hz" liegt. Diese ist im Microwave 2 auf 100Hz angehoben worden, womit interessante Amplituden-, Filter-, sowie Wavemodulationen möglich sind, die FM-ähnlich klingen können! Die LFOs, haben fünf Wellenformen: Zufall, Dreieck, Sinus, Rechteck und Sample & Hold ("S/H"). Diese (S/H-) Funktion nimmt einen Zufallswert an und hält diesen, bis der "LFO - Geschwindigkeitszeitraum" abgelaufen ist, während die Einstellung "Zufall" (random) ständige Änderungen produziert. Die LFOs lassen sich miteinander synchronisieren (Gleichlauf), womit rhythmisch abhängige Modulationen möglich sind. Auch gibt es eine Phasenverschiebung gegeneinander, die in Grad eingestellt wird. Der LFO1 kann zusätzlich in seiner Geschwindigkeit und Intensität auch moduliert werden. Die restlichen Hüllkurven sind in "ADSR"-Bauweise aufgebaut (siehe "3.1.1 Baugruppen"); die Filterhüllkurve hat noch einen Delayparameter vorgeschaltet, der den Pegel auf Null hält, bis die Attackzeit beginnt ("DADSR"). Alle Hüllkurvenparameter sind modulierbar, was extrem flexibel ist und mit sehr wenigen anderen Geräten überhaupt machbar ist! Der Wave und Microwave 2 haben eine zusätzliche erweiterte Hüllkurve, dafür keine Minihüllkurve in LFO1 und kleine Abweichungen bezüglich der Modulation des Delayparameters. Es gibt, wie im Wave auch im Microwave 2, sogenannte Modifier, die verschiedene Bearbeitungen der Modulationssignale zulassen (mathematisch / logische Operationen, Verzögerungsgeneratoren, u.a..) und eine Minihüllkurve ebenfalls simulieren lassen, kurz: vergleichbaren und verbesserten Ersatz bieten. Die Modulationen werden im Microwave 2 über eine (auf 16 Verbindungen) begrenzte Modulationsmatrix bedient, die das Konzept des "allesmodulierenden Monsters" zugunsten der Rechenzeit verringert (es zählt die "Updatezeit", in der alle Werte neu berechnet sind - diese ist zwingend höher für die Geschwindigkeiten der LFOs etc..). Die Oszillatoren können dafür im Microwave 2 synchronisiert werden (Obertonveränderung)!! Außerdem gibt es Ringmodulation, -diese erlaubt metallische Klänge, wie oben beschrieben. Die Oszillatoren-, Wavetable-, Verstärker-, Panorama- und Filterparameter etc... sind allesamt modulierbare Ziele, oft sogar mehrfach. Einige haben "Seitensteuereingänge" ("Sidechains" / "Ctrl. Input"), die die Modulationsquelle durch eine weitere Modulationsquelle steuern können. Z.B. LFO1 wird durch das Modulationsrad in seiner Intensität gesteuert, dieser LFO1 moduliert die Resonanz des Filters. Das Ergebnis ist eine Steuerung der LFO-Modulationsintensität auf den Resonanzparameter durch das Modulationsrad. Als (Modulations-)Quellen stehen (u.a.) zur Verfügung: LFOs, Hüllkurven, MIDI-Controller, die Hüllkurve von LFO1, Keytrack, Anschlagdynamik... Außerdem gibt es zusätzlich oft benutzte, festverdrahtete Modulationsverbindungen, wie Filter-Cutoff (Filtereckfrequenz)-Steuerung durch Filterhüllkurve. Die Oszillatoren können nicht als Modulationsquelle zur Verfügung gestellt werden. Dies ist auch nicht üblich, außer in FM- oder AM-Geräten, die aber wiederum keine Wavetablesynthese anbieten. Durch die schnellen Microwave 2 - LFOs und die Ringmodulation / Sync(hronisation) wird aber soetwas trotzdem möglich! Es gibt noch einige Funktionen für das spezielle Stimmen und Skalieren, sogar ein Programm zur Reinstimmung der Oszillatoren ist im Microwave zu finden: sobald ein Akkord gespielt wird, werden sie auf die "Reinstimmung" dieses Akkordes korrigiert, dies wird "Hermode-Tuning" (hmt) genannt und kann in "Keys 3/95" gehört / nachgelesen werden. Die restlichen Funktionen werden nicht näher beschrieben... sie dienen weiterer Organisation und subtilerer oder speziellerer Klangformung und sind unterschiedlich in den Geräten realisiert. Auch die "SysEx-Steuerung" (= spezielle Befehle über die MIDI Schnittstelle zur kompletten Echtzeitsteuerung eines ganz speziellen Gerätes eines Herstellers) oder die Editierzwischenspeicher (mehrere!) sind keine Normausstattung, dienen aber ebenfalls der schnellen Rahmensprengung dieser Arbeit). Ein letzter, aber sehr kreativer Punkt ist die Computereditierbarkeit der Waves und Wavetables. Es gibt ein additives Verfahren und die sogenannten UPAWs (User Programmable Algorithmic Wavetable = Benutzerprogrammierbare algorithmische Wellentabelle). Im additiven Modus kann eine Wellenform durch Veränderung der ersten 64 harmonischen Teiltöne eingestellt werden (die x-ten ganzzahligen Vielfachen des Grundtons im harmonischen Spektrum). Die resultierende Wave wird dargestellt und kann in einem Wavetable verwendet werden. Der Clou hierbei ist die Dynamisierung der (nun nicht mehr festen) Einzelspektren, die ja beliebig kombiniert werden können.

Die UPAWs benutzen verschiedene Syntheseformen wie FM Sy nt he s e, W av es ha pi ng (e tc. ..) u m W av etables zu errechnen, dabei gibt man zuvor die zugehörigen Parameter an und läßt so einen Wellensatz durch den Computer "offline" (nicht in Echtzeit) ausrechnen. Eine Mischung mit "normalen" Waves ist allerdings nicht möglich. Der Waldorf Wave kann zudem ein Sample in den Speicher holen und es in ein Wavetable umrechnen lassen, dabei wird das Sample in soviel gleiche Teile aufgeteilt, wie es Waves in einem Wavetable gibt, und für diese "Gesamtteilzeit" wird ein additives Spektrum errechnet (mit der "Fourieranalyse") und eine Wavetable gebildet.

Der analysierte Zeitraum ist: Samplelänge dividiert durch Anzahl der Waves in einem Wavetable.

Wenn das fertige Ergebnis nun durchfahren wird, hat man ein upaw"ungefähres" Abbild des analysierten Samples. Diese und andere Offlinealgorithmen können benutzt werden, manche im Wave sogar direkt nach Knopfdruck abhörbereit! Der Wave arbeitet mit einem Multiprozessorsystem (MC68000) und hohen Taktfrequenzen. Beim Computer und Microwave (2) - Verbund ist die Übertragung und Verarbeitung noch "dazwischen" und "bremst" etwas. Soviel zu den wichtigsten Waldorfer Techniken. Das Wavesequencing der Korg Wavestation funktioniert nach einem ähnlichen System, allerdings mit Samples: Diese werden "anstatt" der Wellentabellen durch die Hüllkurve angewählt und bei Wechsel zu einem anderen Sample (durch einen anderen Modulationssteuerwert) in das dazugehörige, nächste Sample überblendet, hier wirklich überblendet und nicht "gemorpht". Man hat hier auch eine Liste der Einzelsamples zu erstellen, was dem Waldorf - System prinzipiell nahe ist.

3.3 Weitere Algorithmen: zB physical modeling (zB. yamaha vl1) und fm-synthese (zB. DX7)

Eine absolut vollständige Beschreibung aller existenten Synthesen und Baugruppen ist (in diesem Rahmen) nicht möglich, daher wurde die hier vorliegende Art dieser Arbeit gewählt. Für weitere Informationen empfehle ich einen Blick in die Fachliteratur und Experimentieren mit den Geräten und Programmen, insbesondere für grundlegende Themen wie Filterbau, etc... Eine Technik, die nicht unerwähnt sein darf, ist die FM-Synthese (Frequenzmodulation), welche vor allem in Yamahas DX Serie, ab 1983, u.a. in Form des wohlbekannten "DX7" Anwendung fand. Hier sind Oszillatoren (bei Yamaha "Operator" genannt), in einer bestimmten Weise miteinander verknüpft (Yamaha nannte dies "Algorithm". algorithmus FM

Die Anzahl der Oszillatoren war bei den meisten Geräten auf sechs oder vier pro Stimme festgelegt (Die DX und TG / SY serie bis zum FS1R von Yamaha).. Jeder Oszillator hat eine Lautstärkenhüllkurve und kann in ihrem Frequenzverhältnis zu den anderen Oszillatoren jeweils eingestellt werden, da dies entscheidend für die Klangformung ist: Der unterste der Oszillatoren "in einem Strang" (Algorithm) ist der sogenannte Träger, der durch seine Hüllkurve ein- und ausblendbar ist und für den Lautstärkenverlauf sorgt. Der nächste Oszillator, der den Träger in seiner Frequenz steuert, der Modulator, kann nun durch seine Hüllkurve (obwohl sie, nach wie vor, die Lautstärke dieses Modulators steuert) den Klang verändern, da er ja die Frequenz des Trägers steuert, mit der Intensität des aktuellen Hüllkurvenpegels. Nun kann auch der nächste Oszillator den modulierenden Oszillator abermals modulieren und durch seine Hüllkurve für eine komplexere dynamische Klangsteuerung sorgen. Sechs nebeneinander liegende (parallele) Träger sind genauso möglich (wie bei einer Zugriegelorgel einfach 6 ein- und ausblendbare Töne einer festen Frequenz / keine FM), wie auch sechs sich gegenseitig modulierende, lediglich festgelegt. Durch den "Algorithm", ein Schaltbild, welches sich auswählen und sogar im Falle der TG /SY (77 und 99) - Modelle frei definieren läßt, kann man alle parallelen und seriellen Kombinationen ausschöpfen. Die mathematischen Grundlagen dieser und anderer Synthesetechniken sowie der Interpolation sind sehr weitreichend und können unter anderem im "Taschenbuch mathematischer Formeln" von Dr. Ing. Hans-Jochen Bartsch, ISBN 3-343-00876-1, Fachbuchverlag Leipzig - Köln ausführlich untersucht werden. Die additive Synthese findet zur Zeit neue Beliebtheit in Form der Kawai K5000-Serie, dem "Emulator IV" (bedingt) und Computersystemen wie etwa "Kyma" und "Generator".. Hier werden eine Anzahl von meist 64 oder 128 Obertönen (Teiltönen) mit je einer Hüllkurve versehen(!) und einzeln editiert(!). Die Zusammensetzung dieser Teiltöne (in "Reintheorie" Sinusschwingungen der x-ten Vielfachen des Grundtons!) ergibt den komplexen Gesamtklang und erhält seinen Namen aufgrund der Addition der Einzelteiltöne. Wenn man eine dreidimensionale Landschaft (entsprechend den Achsen: Amplitude, Frequenz und Zeit) aufgezeichnet hat, so bekommt man einen Eindruck dieser Synthese: Die Amplituden über der Zeit (ein zeitlicher Hüllkurvenverlauf der Amplitude einer Frequenz / die zweite Dimension im Gebirge) sind einzelne Scheiben in diesem Gebirge. Jede Scheibe steuert die Lautstärke eines Oszillators einer bestimmten Frequenz, der dritten Dimension in diesem Gebirge entsprechend. Nachteile sind: sehr viele Parameter, denn, genaugenommen, müssen noch diese Dinge geschaffen werden:- Phasensteuerungshüllkurven- Frequenzhüllkurven

• Gegen "unendlich" viele Oszillatoren, auch mit nicht ganzzahligen Frequenzen
• Jemand, der dies überschauen kann

In der Praxis werden Makros (Ein Befehl für viele Einzeloperationen) benutzt, dafür keine der genannten letzten Punkte realisiert (bisher). Kawai versucht es mit einem Spektrum, welches als "Filter" vom aktuellen Spektrum subtrahiert wird und beweglich ist (frequenzmäßig), dadurch ist ein quasi "charakteristikprogrammierbares" Filter entstanden. Mathematisch ist hier eine (Fourier-)Reihe der einzelnen Sinusfunktionen pro Teilton zu bearbeiten, dessen Umfang ebenfalls enorm ist und durch externe, o.a. Literatur eingesehen werden kann. Der Anwender bekommt natürlich das mathematische Innenleben seiner Geräte nicht mit. -Einen kleinen Eindruck dessen bekommt man jedoch bei Ansicht der Filterkonstruktion (Kapitel 3.1.1.). Korgs Prophecy gab man gleich diese Synthesen mit: FM, subtraktive, VPM (Phasenmodulation), Sync./Ring/Xmod, Waveshaping etc.. und eine Entwicklung der neueren Zeit zeichnet sich neben vielen subtraktiven und additiven Mischarten der Klangerzeugung ab: das "physical modelling". Aufgrund der physikalischen Grundlagen eines akustischen Instrumentes wird ein Algorithmus angewendet, der sich oft auch aus der "real üblichen" Parameterisierung entfernt, jedoch an die physikalisch-mathematischen Grundlagen der Originalinstrumente angelehnt ist. So kann aus dem physikalischen Algorithmus ("Modell") einer gezupften Saite und einer Luftsäulenschwingung (mit Resonanzraum), aus einem "Flötenmodell" eine "gestrichene Flöte" werden, u.ä. Die so gewonnenen Klänge haben oft ein Höchstmaß an Authentizität bei "wenigen" Parametern, denn die Rechenvorschrift ist ja eine genaue naturwissenschaftliche / mathematische Beschreibung des akustischen Instrumentes. Vertreter dieser Gerätegeneration sind Yamahas VL1, VP1 und VP70m (gegen die die Prophecy-Modelle eher Versuche sind) etc.. Das Selberschaffen dieser Algorithmen erfordert also entsprechende fundierte Kenntnisse im akkustisch / physikalischen Bereich. Man benutzt die vorgegebenen Parameter. Natürlich ist bei allen Syntheseverfahren in realen Systemen immer nur eine "Teil-Authenzität" anzunehmen, denn das "Original" kann aufgrund seiner physikalischen Existenz nicht zu 100% realisiert werden, jedoch ist (wie generell in der Synthesizertechnik) auch nicht der Ersatz der traditionellen Instrumente das Ziel, allenfalls deren "Simulation" und Verbesserung, um eine Musik Produktion schneller und unkomplizierter zu realisieren. (Bei entsprechender Spielweise kann ein "Modell" trotzdem sehr "echt" klingen.) Die Stärken der synthetischen Klangerzeugung sind neue, vorher "ungehörte" Klänge. Beim physical modelling Fm syntheseist man jedoch sehr gefordert, wenn man dies einfach "heraushören" will. Nichtsdestotrotz ist das wirklich Interessante dieser Technik, die "Grenzbereiche" der Modelle zu finden und sie für ein neues virtuelles akustisches Instrument zu verwenden, das wohl real nie gebaut werden wird.

Dies sind: Algorithmus mit 2 Trägern, der untere Strang wird moduliert. Op.2 von Op.4 und Op.6 etc.. (rechts) und ein Ausschnitt aus dem Hüllkurventeil sowie der Keyboardskalierung eines Yamaha TG77 (links: synthDB)

3.3.1 Softwaresynthesizer

(Stand der Urfassung: 1997) Wie sicher schon zu erkennen war, stellt diese Gattung die Zukunft und die Gegenwart der digitalen Synthesizer dar. Die unspezifische "Verpackung" (Gehäuse) eines Computers als Synthesizer ist natürlich für ein offenes System geeignet. Der Native Instruments "Generator" ist ein Modular - Synthesizer, der komplett auf einem Pentium Rechner (mind. 100 Mhz) "läuft" und in seiner Komplexität und Parametrisierung nur durch die vorhandenen Module (Software), die Kreativität des Benutzers, sowie die Rechenleistung beschränkt wird: Ein Synthesizer der Komplexität eines Sequential Prophet 5 kann auf einem 133Mhz - Pentium - Rechner etwa 6 bis 8 Stimmen haben. Man kann nun "30 LFOs hinzufügen" oder einen "25sten Oszillator frequenzmodulierend wirken lassen" etc.., solange es der Rechner zuläßt (performancemäßig)!

Das zur Zeit leistungsfähigste System, das den Begriff des "Synthesizers" besonders für sich verbuchen kann, dürfte Kyma sein (von Symbolic Sound, USA). Hier gibt es jede oben angedeutete Freiheit, die man möchte. Das System ist ein "Capybara 66" genannter "DSP - Mainframe" (also eine Digital Signal Prozessor - Basiseinheit), mit max. 8 Stück Motorola (56002) Signalprozessoren mit 66MHz Taktfrequenz , der über den Computer (Mac oder PC) gesteuert wird. Diese Prozessoren sind besonders für Synthesizeroperationen geeignet und sind, zum Vergleich, in ihrer 40Mhz - Version (also etwas langsamer) dreifach im Nord Lead zu finden. Da Kyma auch über analoge Eingänge und Ausgänge, sowie eine MIDI- Schnittstelle verfügt, ist er Sampler, Synthesizer, (Harddisk = Festplatten-) Rekorder und Effektgerät in einem, das auch über einen normalen Sequencer gesteuert werden kann. Dieser Sequencer kann auf dem Computer ebenfalls "mitlaufen", denn die Hauptarbeit wird in den DSPs erledigt.

Eine Vielzahl von Software - "Modulen", die ständig erweitert werden, sind hier einsetzbar. Auch Vocoder (eine Art "Stimmensynthesizer" auf Basis von Filtern) oder Hall sind vorhanden wie Hüllkurven und Filter usw..

Will man nun einen FM-Synthesizer erzeugen, kann man sich hier einen generieren und benutzen. Man kann nun zu jedem Klang den benötigten Synthesizer entwerfen, indem man die Module am Bildschirm mit der Maus auswählt und in eine grafische Signalflußkette einsetzt, die auch Analogeingänge und Festplattendateien in Echtzeit erfaßt. Die Parameter dieser Module können fest eingestellt werden oder durch MIDI oder andere Module gesteuert werden. Es entspricht einem analogen Modularsystem für den Anwender, wenn seine Technik auch völlig anders ist. Die Verquickung der Effektprozessoren, dem Synthesizerteil und dem Rekorder mit dem Sequencer in einem Gerät wird sicherlich ein Konzept der Zukunft sein; denn man kann so auch z.B. physikalische Modelle konstruieren: eine Verzögerungstrecke kann, wie auch ein "Resonator" (ein simulierter Resonanzraum, z.B. von einer akkustischen Gitarre), leicht mit den "üblichen" Modulen (Oszillatoren etc..) verbunden werden und mit einer Rückkopplung versehen werden. Diese sind im Kapitel über Baugruppen und Filterschaltungen angedeutet! Natürlich auch speziellere Dinge. Stichwortartig erwähnt seien: Granularsynthese, spektrales Morphing zwischen Sounds, Modulieren bestimmter harmonischer Obertöne etc.. Diese Dinge werden nicht erklärt, sondern nur aufgeführt, um das zukünftige Prinzip der Synthesizer zu erklären, da die Seitenzahl dieser Arbeit mehrbändigen Lexika zur Konurrenz wird..

Dies ist zugleich der Beginn der Schlußbetrachtung, denn hier läßt sich die Zukunft schon deutlich erkennen:

Brauche ich oben erwähnten FM-Synthesizer, so nehme ich mit der Maus entsprechend viele Oszillatoren und verknüpfe deren (Frequenz-)Steuerein-/ausgänge miteinander; die Lautstärken werden durch die Hüllkurven gesteuert, die ich aus einer Bibliothek der Module nehme, etc...

die folgenden Schritte ergeben sich einfach aus der verwendeten Technik und müssen sicher nicht mehr kommentiert werden...

Interessant wird so etwas, wenn die unkonventionellen Module noch dazugenommen werden, denn hier beginnt das, wo andere Synthesizer festgelegt sind, z.B.: "Granularsynthese mit einigen Bandpässen" und "Hüllkurven" und "anschließender spektraler Verformung" etc...

5.CD Inhalte

hier downloaden: http://www.sequencer.de/synthaudio/synthesizer_cd_literatur.html#synthdiplomAUDIO

6. Literaturverzeichnis

5. Literaturverzeichnis

monatliche Zeitschriften:

- Keys 1/97, PPV Presse Project Verlags GmbH, Bergkirchen-

Keyboards 4/86, 5/86, 6/86 MM-Musik Media Verlag GmbH, Augsburg

sowie die Informationen dieser Zeitschriften seit 1985...

Bücher:

- Marc Vail, Vintage Synthesizers, 1. Auflage, 1993, GPI / Miller Freeman Books San Francisco

- Dr.Ing. Hans-Jochen Bartsch, Taschenbuch mathematischer Formeln, 16.Auflage 1994, Fachbuchverlag Leipzig-Köln Leipzig

- Matthias Becker, Synthesizer von gestern, 1. Auflage, 1990, MM-Musik Media Verlag Augsburg

- Europa / H.Häberle, Tabellenbuch Elektrotechnik, 11.Auflage, 1984, Verlag Europa Lehrmittel, Nourney, Vollmer, Wuppertal

Verschiedenes:

- Informationen und Bedienungsanleitungen der exemplarischen Firmen Waldorf, Symbolic Sound, Clavia

- sowie sehr viele persönliche Informationen / Aufzeichnungen des Autors..

... 6. Bilderverzeichnis

Seite 4 - Foto: YAMAHA CS-80 (fotografiert von Dieter Stork) Matthias Becker, Synthesizer von gestern, Seite 71 unten rechts, 1. Auflage, 1990, MM-Musik Media Verlag Augsburg

Seite 6 - Grafik / Prinzipskizzen: vom Verfasser selbst (analog <>digital)

Seite 8 - Foto: vom Verfasser selbst (diverse Synthesizer)

Seite 18 - Foto: vom Verfasser selbst (CLAVIA Nord Lead, offen)

Seite 21 - Foto: vom Verfasser selbst (WALDORF Microwave, offen) Foto: vom Verfasser selbst (YAMAHA TG77, offen)

Seite 25 - Grafik / Skizzen: vom Verfasser selbst (Filterkennlinien)

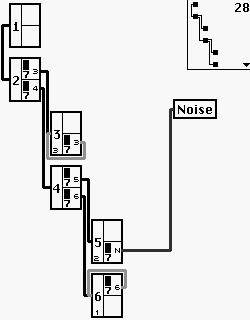
Seite 28 - Grafik: vom Verfasser selbst (WALDORF Microwave Parameter für Modulationen, Oszillatoren, LFOs & LFO-Hüllkurve, Mix, Wave/table)

Seite 35 - Grafik: vom Verfasser selbst (WALDORF Microwave: Wavetable-Ausschnitt / Interpolation, Wave-Hüllkurve, Filter-Hüllkurve mit Modulationen)

Seite 38 - Grafik: vom Verfasser selbst (Beispiel für FM-Synthesizer: Hüllkurven, Skalierung und "Algorithm" für YAMAHA TG77)

Anmerkung: Einige Grafiken wurden unter Zuhilfenahme des Programms "EMAGIC Sounddiver für Apple Macintosh" erstellt.

7. Bilderverzeichnis

8. Anhang (Demo-CD Inhalt) AUDIO DOWNLOAD

9 ) find a complete "how to make a bass with FM" tutorial here / Tutorial für FM Bass Sounds hier..