amesser
||||
Moin,
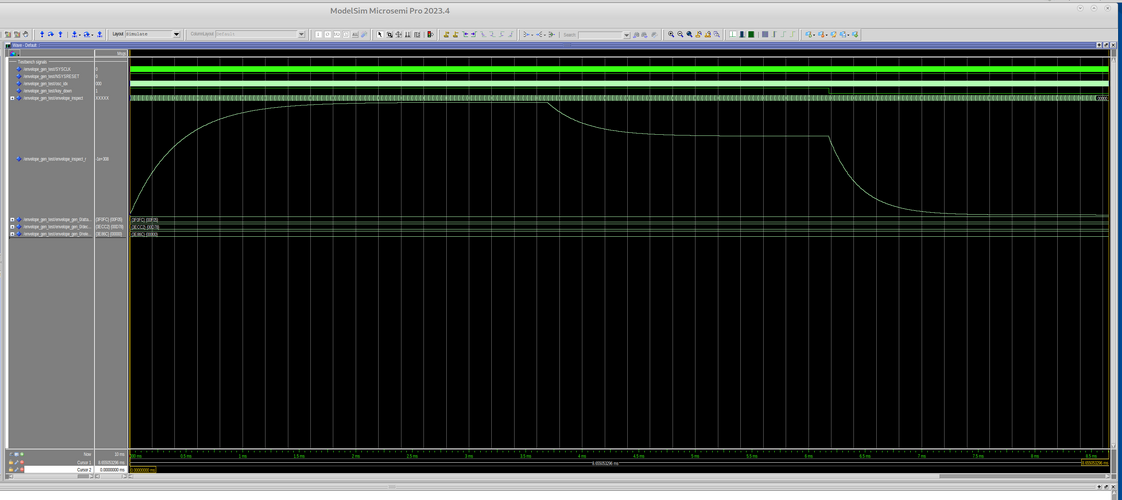
ich lass euch mal an meinen Gedanken teilhaben. Bin hier eher als Techniker statt als Musiker unterwegs und versuche mich gerade daran einen Synthesizer im FPGA zu implementieren. Der DX-7 dient so ein bischen als Vorlage. Die Oszillatoren laufen schon, jetzt bin ich an den Hüllkurven dran. Dabei komme ich jetzt so ein bischen an die Grenzen der Genauigkeit der Berechnung. Da tun hier gerade lange Zeiten der einzelnen Stufen von so einer Hüllkurve weh. Ich habe da jetzt mal von einem minimalen Attack von 10µs ausgehend simuliert. Da komme ich bis etwa 400ms Attack, ab da wirds dann zu ungenau. Natürlich könnte ich die Genauigkeit der Berechnung erhöhen, das kostet mich aber viele Resourcen im FPGA. (Der hat DSP Blöcke für 18 Bit, bei höherer Genauigkeit braucht man dann gleiche viel mehr davon)
Jetzt meine Frage an die Musiker: Welche Zeitbereiche sind denn für die Hüllkurvensegmente sinnvoll? Wenn ich z.B. erst bei 50µs starte, dann treten die Rechenfehler erst ab 2.5s auf. Ich habe mal verschiede Anleitungen von aktuellen Synths gewälzt, aber da stehen meist keine konkreten Zahlen für die Hüllkurven drinnen. Eine weitere Möglichkeit wäre es, dass ich eine (wählbare) Untersetzung der Rechenschritte einbaue. Das entspricht dann so ungefähr dem Kippschalter den man auf vielen Eurorack ADSRs findet. Das hätte dann halt die Folge, das bei langen Zeitbereichen die Kurve möglicherweise "stufig" umschaltet. Allerdings, im Moment wird alle 7µs ein neuer Hüllkurvenpunkt gerechnet, bei einer Untersetzung 1:100 wären das immer noch alle 0.7ms ein neuer Punkt, das hört man dann wohl eher nicht. und ich käme bis auf 50s hoch.
Was meint Ihr? Schonmal danke für den Input. (Und ja meine Hüllkurven sind im Moment so schnell, das die eigentlich Audio sind, wohl vollkommen übertrieben, aber der Döpfer kann auch 20µs)
Grüße,
Andreas
ich lass euch mal an meinen Gedanken teilhaben. Bin hier eher als Techniker statt als Musiker unterwegs und versuche mich gerade daran einen Synthesizer im FPGA zu implementieren. Der DX-7 dient so ein bischen als Vorlage. Die Oszillatoren laufen schon, jetzt bin ich an den Hüllkurven dran. Dabei komme ich jetzt so ein bischen an die Grenzen der Genauigkeit der Berechnung. Da tun hier gerade lange Zeiten der einzelnen Stufen von so einer Hüllkurve weh. Ich habe da jetzt mal von einem minimalen Attack von 10µs ausgehend simuliert. Da komme ich bis etwa 400ms Attack, ab da wirds dann zu ungenau. Natürlich könnte ich die Genauigkeit der Berechnung erhöhen, das kostet mich aber viele Resourcen im FPGA. (Der hat DSP Blöcke für 18 Bit, bei höherer Genauigkeit braucht man dann gleiche viel mehr davon)
Jetzt meine Frage an die Musiker: Welche Zeitbereiche sind denn für die Hüllkurvensegmente sinnvoll? Wenn ich z.B. erst bei 50µs starte, dann treten die Rechenfehler erst ab 2.5s auf. Ich habe mal verschiede Anleitungen von aktuellen Synths gewälzt, aber da stehen meist keine konkreten Zahlen für die Hüllkurven drinnen. Eine weitere Möglichkeit wäre es, dass ich eine (wählbare) Untersetzung der Rechenschritte einbaue. Das entspricht dann so ungefähr dem Kippschalter den man auf vielen Eurorack ADSRs findet. Das hätte dann halt die Folge, das bei langen Zeitbereichen die Kurve möglicherweise "stufig" umschaltet. Allerdings, im Moment wird alle 7µs ein neuer Hüllkurvenpunkt gerechnet, bei einer Untersetzung 1:100 wären das immer noch alle 0.7ms ein neuer Punkt, das hört man dann wohl eher nicht. und ich käme bis auf 50s hoch.
Was meint Ihr? Schonmal danke für den Input. (Und ja meine Hüllkurven sind im Moment so schnell, das die eigentlich Audio sind, wohl vollkommen übertrieben, aber der Döpfer kann auch 20µs)
Grüße,
Andreas