Puls-Wellenform: wie verstehe ich diese Abbildung?

[NickLimegrove]

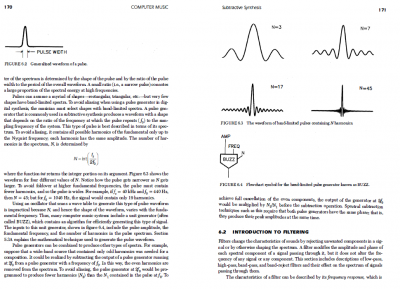
In einem schön gemachten, sehr spannenden (leider didaktisch nicht so doll aufbereitetem) Buch finde ich die folgende Abbildung, die vier Wellen oben rechts (6.3).




Natürlich kenne ich verschiedene Wege, ein Klangereignis zweidimensional zu visualisieren, aber hieraus werde ich nicht ganz schlau -- vor allem: was zeigt denn die x-Achse? Frequenzen wie in einem Spektrogramm ja wohl kaum. Die Zeit, wie bei den üblichen Wellenform-Darstellungen? Oder was ganz anderes? Wenn die Zeit: müsste man das dann so lesen, dass ein ›Puls‹ zunächst eine gemütliche Einschwingphase um die Nulllinie herum hätte, dann kommt der eigentliche Puls, asymmetrisch weit über 0 hinaus, aber kaum darunter, und dann wieder eine gemütliche Ausschwingphase? Wenn ja, wo käme dann dieses komische Einschwingen her? Ich komme hier, gedanklich, irgendwie nicht vom Bild zum Ton...

danke für jeden Hinweis!

 

[NickLimegrove]

Re: Pulswellen: wie verstehe ich diese Abbildung?

PS: Dodge/Jerse (1985/97): ›Computer Music‹

 

[Summa]

Re: Pulswellen: wie verstehe ich diese Abbildung?

Willst du deinen eigenen Synth programmieren?

 

[Xpander-Kumpel]

Re: Pulswellen: wie verstehe ich diese Abbildung?

Doch, Du siehst eine Spektraldarstellung mit unterschiedlichen Anzahlen von Harmonischen Schwingungen(ganzzahlige Vielfache/Teile der Grundschwingung) "n" gibt dabei die Anzahl der harmonischen+1 Grundton an. Der Peak in der Mitte ist der Grundton. So würde ich das jedenfalls sehen. Jede Schwingung kann additiv aus mehreren Sinusschwingungen zusammengesetzt werden. Im Casio FZ-1/FZ-10 hatte ich mal wunderbare Pulsesounds mit linear absinkenden ungeraden Harmonischen hingekriegt, kann man mit der Kiste einfach "malen".

 

[Xpander-Kumpel]

Re: Pulswellen: wie verstehe ich diese Abbildung?

Aus der Spektraldarstellung kann man auf den ersten Blick eigentlich nicht erkennen um was für eine Wellenform es sich im Zeitbereich(z.B. Oszilloskop) handelt.
Nur den reinen Sinus erkennt man sofort, weil der nämlich keine Obertöne hat.

Bei allen anderen Standartwellenformen müßte man die Harmonischen auszählen und schauen um wieviel dB sie abgesenkt sind um festzustellen welche Wellenform(aufm Oszilloskop) das ist.
(es gibt auch mathematische Transformationen mit denen man vom Zeit- in den Frequenzbereich umrechnen kann, Fouriernalyse oder LaPlace-Transformation)

Der erklärt aber auch schön warum nicht alle Sägezähne oder Sinen oder Pulsen gleich klingen, sie haben nämlich unterschiedliche Spektralanteile und eine "Verschmutzung" mit zusätzlichen Harmonischen klingt oft interessant.

In der FM-Synthese finde ich persönlich das sich mit "reinen" Sinusschwingungen oft viel bessere Ergebnisse erzielen lassen als mit "dreckigen" Wellen.

 

[Xpander-Kumpel]

Re: Pulswellen: wie verstehe ich diese Abbildung?

...der Artikel geht übrigends nicht von einer "Pulswelle" wie wir sie hier oft verstehen(Rechteckschwingung) aus, sondern meint eine Impuls-artige Schwingung.

Und die Darstellungen zeigen also keinen Schwingungsverlauf im Zeitbereich(X-Ache = Zeitverlauf, Y-Achse = Amplitude/Lautstärke) sondern das Spektrum einer Schwingung/Darstellung im Frequenzbereich(X-Ache = links tiefe Frequenzen aufsteigend nach rechts hohe Frequenzen, Y-Achse = Amplitude/Lautstärke) mit "n"=Anzahl der Einzelschwingungen die diese komplexe Gesamtschwingung bilden.

 

[NickLimegrove]

der Artikel geht übrigends nicht von einer "Pulswelle" wie wir sie hier oft verstehen(Rechteckschwingung) aus, sondern meint eine Impuls-artige Schwingung.

Ja, da war das Wort ›Pulswelle‹ im Threadtitel vielleicht etwas misleading, hab's jetzt geändert...

Okay, also du würdest sagen, doch Spektrogramm. Ich hatte das auch überlegt (z.B. weil sich die N-Werte so schön in den Anzahlen der vermeintlichen Schwingungen spiegeln), dann aber wieder verworfen, weil ich dachte: die Frequenzen in einem Spektrogramm würde man ja wohl eher diskret darstellen, also mit klar abgegrenzeten Bänden, wie man's aus den typischen Darstellungen z.B. im FM-Dunstkreis kennt.

Aber klar, man kann die Frequenzen natürlich auch kontinuierlich darstellen. Nur blöd, wenn der Leser so sehr auf die klassischen Wellen-Plots konditioniert ist, dass er, sobald er was wellenartiges sieht, sofort meint, das müssen Schwingungen auf einer Zeitachse sein

 

[Xpander-Kumpel]

So würde ich es deuten, hier gibts ja noch ein paar Profis für dieses Thema die wissens bestimmt noch genauer.
Ich finds auf jeden Fall irgendwie geil, diese Zusammenhänge, ist schon faszinierend.

 

[Cyclotron]

Das ist die Darstellung des Impulses links oben in bandlimitierter Form. Wenn an Deinem AD Wandler das linke Signal ankommt, wird es gefiltert und danach gesamplet. Das Ergebnis ist dann rechts zu sehen. Sinn der Sache ist es, Frequenzen oberhalb der Nyquistrate auszufiltern, denn der Impuls in seiner ursprünglichen Form enthält Frequenzen, die zu Aliasing führen.

 

[Xpander-Kumpel]

...müßte man dann nicht dazu noch erklären das das Signal, um "n" zu senken Bandpass-gefiltert wird?
Bedenke hier sind ja wenig Profis unterwegs .
(Harmonische "rechts" und "links" wegfiltern)

Ein Low-Pass-Filter filter "rechts" weg, ein High-Pass filter "links" weg und der Bandpass-Filter der eine Verbindung von Low und Hi ist kann das beides.

 

[starling]

https://de.wikipedia.org/wiki/Sinc-Funktion

 

[weird fish]

X ist Zeit / Y Amplitude. Hier sieht man das etwas besser:
https://www.cs.sfu.ca/~tamaras/subtractSynth/Band_Limited_Pulse_Generato.html

 

[Xpander-Kumpel]

X ist Zeit / Y Amplitude. Hier sieht man das etwas besser:
https://www.cs.sfu.ca/~tamaras/subtractSynth/Band_Limited_Pulse_Generato.html

Ich würde sagen obwohl dort Zeit(t) auf der Achse steht, ist es eigentlich die Frequenz(kenne diese Bilder oft mit der Angabe der Kreisfrequenz z.B.) die dort dargestellt ist.
Eine Frequenz ist natürlich auch zeitabhängig aber stellt nicht die Zeit dar.
Für mich sieht das falsch aus.

Eine Harmonische schwingt doch nicht zeitlich nach oder vor dem Grundton?

 

[Bug2342]

Ich versuch mich auch mal als Erklärbär:

Die Darstellungen sind in der "normalen" Wellenformdarstellung, also links/rechts: Zeit; oben/unten: Amplitude.

Die Pulswelle ist hier eine Impulswelle, also eine Pulswelle mit Pulsweite ganz nah an der 0, so dass es (in der nicht bandlimitierten Variante) nur einen "unendlich" kurzen Puls nach oben gibt. In der Frequenzdarstellung hätten der Grundton und jeder der Obertöne (schon wieder bis zum "unendlichsten" Oberton) die gleiche Amplitude.

Wenn man das nun samplen wollte bzw. einen Impuls berechnen und ausgeben, wäre das Mist, weil man da natürlich Aliasing hat, bis der Arzt kommt. Drum verwendet man (manchmal) sogenannte bandlimitierte Wellenformen. Im Frequenzraum sind die relativ einfach herzustellen, man schmeißt nämlich einfach alles oberhalb eines bestimmten Obertons (das n in den Bildern) weg (d.h. man setzt die Amplituden für die hohen Obertöne auf 0). Das führt wiederum dazu, dass man keine scharfen Kanten hat, wenn man das in die normale Zeitdarstellung rücktransformiert, sondern das komische Geeier vor und nach der Wellenform.

Wo man den Kram z.B. braucht ist, wenn man bandlimitierte (d.h. nicht aliasende) klassische Synth-Wellenformen generieren möchte. Ein bandlimitierter Puls ist überaschenderweise recht einfach zu berechnen (man braucht glaube ich eine audio-rate Division, ist also nicht ganz billig in Sachen Rechenzeit). Schiebt man den z.B. durch einen Integrator, fällt (bis auf einen DC-Offset) ein wunderhübscher bandlimitierter Sägezahn raus.

Hoffe das Hilft...

 

[Cyclotron]

Eine Harmonische schwingt doch nicht zeitlich nach oder vor dem Grundton?

Das ist schon korrekt. Sowas kannst Du z.Bsp. auch wunderbar bei phasenlinearen Filtern sehen, wen Du ein einziges Sample (einen "Knacks", auch Rechteckimpuls genannt) durchschickst. Das ist dann die Impulsantwort des Filters.

 

[Xpander-Kumpel]

Also ist das quasi eine Darstellung eines "Zeitfensters" und alle "teilnehmenden" Töne sind in zeitabhängiger Darstellung übereinandergelegt(gleicher Nulldurchlauf)?

ich kapier es nicht.
Das Bild sagt doch dann aus das dieser Impuls sich mit einer bestimmten Frequenz einschwingt, dann auf die Peaknadel geht und dann symmetrisch zum Einschwingen aussschwingt?

 

[swissdoc]

Es geht um die Erzeugung einer bandlimitierten Pulse-Schwingungsform. Man sieht die Zeitdarstellung. In dem Link hier: https://www.cs.sfu.ca/~tamaras/subtract ... erato.html
sind oben die Zeitreihen, also Amplitude über die Zeit und unten die Amplituden der ersten 45 Harmonischen angegeben (leider mit einer Liniengrafik, was ein kontinuierliches Spektrum suggeriert).

Wenn man einen Pulse einfach so als Kasten nimmt, dann bekommt man Aliasing ohne Ende, das Spektrum ist eben dort nicht limitiert. Im Kontext von Musik mit dem Computer ist man immer digital mit Samples unterwegs und muss sich um das vermeiden von Aliasing einige Gedanken machen.

Wer mehr zum Thema sucht, suche unter BLIT oder Band Limited Impulse Train, ein nettes Paper ist Alias-Free Digital Synthesis of Classic Analog Waveforms von Tim Stilson und Julius Smith (der PM Pabst)

Es gibt auch ein VST, das BLIT einsetzt: http://www.kvraudio.com/product/polyibl ... on/details

 

[Xpander-Kumpel]

...also Ihr Profis habt nun dreimal die gleiche Grafik gepostet, aber erklären was man dort sieht für Lernbehinderte wie mich ist scheinbar schwer, wenn man selber weiß was dort zu sehen ist, oder ?

 

[starling]

Was Du siehts sind einfach gleichlaute Sinusschwingungen in harmonischem Abstand mit entsprechender Phase aufeinandergelegt.

Bzw, und das ist daselbe, die Funktion Sinus (x)/x, mit Skalierungen für x.

Das macht einen Impuls, der eben symmetrisch vor- und nachschwingt. Im Prinzip unendlich lange, wenn auch schnell sehr leise.

Alles was gesamplet ist besteht aus lauter solchen Impulsen, übereinandergelegt.

 

[swissdoc]

Lesen kannst Du aber schon, oder?
Von links nach rechts läuft die Zeit (x-Achse), von unten nach oben (y-Achse) der Pegel. Man sieht einen Puls.

 

[Xpander-Kumpel]

...hm, also ich probiers nochmal.

Die vier Grafiken rechts zeigen den links idealisiert gezeigten Impuls mit verschiedenen Badpassfiltern bearbeitet und dadurch bandbreitenbeschnitten und um Harmonische limitiert?

 

[starling]

Mit verschiedenen Tiefpassfiltern. Kann man so sagen, zwar sind die nicht so gefilter sondern so erzeugt, mit Fouriertransform.
Das spielt aber keine Rolle, das Ergebnis ist exakt dasselbe.

EDIT: exakt dasselbe, wenn der Filter perfekt ("Brickwall") ist soll das heißen.

 

[Xpander-Kumpel]

...ja quatsch Bandpass, Lowpass iset!
Ich habs jetzte glaub ich, man schwere Geburt ....

 

[Xpander-Kumpel]

...ist denn so ein Impuls "alltäglich"?
Der ist ja schon irgendwie komisch, beginnt mit leisen hohen Frequenzen dann kommen mehr tiefe Frequenzen dazu ->gipfelt im lautesten Punkt mit noch mehr Frequenzen und dann hört er genauso auf wie er anfing. Ist das ein realistischer Impuls, oder benutzt man den mehr zum Rechnen?
Oder will man das Signal so hinbiegen?

 

[swissdoc]

Vielleicht hilft noch ein anderes Beispiel, das selbe bei einer Rechteckwelle:

 

[swissdoc]

...ist denn so ein Impuls "alltäglich"?

In gewissem Sinne schon. Audio ist heute ja i.d.R. digital und diese Theorie steckt da einfach drinnen. Ohne das kein mp3 z.B.

Der ist ja schon irgendwie komisch, beginnt mit leisen hohen Frequenzen dann kommen mehr tiefe Frequenzen dazu ->gipfelt im lautesten Punkt mit noch mehr Frequenzen und dann hört er genauso auf wie er anfing. Ist das ein realistischer Impuls, oder benutzt man den mehr zum Rechnen?

Du hast da noch einen Knoten im Kopf. Man sieht die Zeitreihe, nicht das Spektrum, die Frequenzen sind alle gleich stark, allein die Anzahl variert.

Oder will man das Signal so hinbiegen?

Wenn man kein Aliasing will, so muss man die Bandbreite limitieren, geht mit BLIT recht einfach.

 

[starling]

...ist denn so ein Impuls "alltäglich"?
Der ist ja schon irgendwie komisch, beginnt mit leisen hohen Frequenzen dann kommen mehr tiefe Frequenzen dazu ->gipfelt im lautesten Punkt mit noch mehr Frequenzen und dann hört er genauso auf wie er anfing. Ist das ein realistischer Impuls, oder benutzt man den mehr zum Rechnen?
Oder will man das Signal so hinbiegen?

Wie soll man sagen?
Es ist in so fern kein realistischer Impuls, als reelle Signale kausal sind, dh sie haben einen Anfang.
Man kann denselben Puls mit anderen Phasen machen, dann wird er kausal, dh er geht erst laut hoch und schwingt dann (unendlich) aus.
Das wäre dann ein "echte Welt" bandlimitierter Impuls. zB in einem Filter nach dem DA Wandler in einer Soundkarte.

Beide sind bis auf die Phasen eigentlich dasselbe.

Den hier nimmt man zum Rechnen, und zum Filtern, und so will man auch sein Signal in vielen Fällen hinbiegen.
Jedes einzelne Sample in einem Soundsample verkörpert so einen Impuls, dh dort wo Du ein einzelnes Sample
(1 Wert) vermuten würdest liegt "in echt" so ein unendlicher Impulse überlagert vom nächsten ein Sample weiter...
Dh das Signal besteht eigentlich aus lauter solchen bandlimitierten Impulsen.
Wobei es in etlichen Fällen egal ist ob Du die symmtrische oder die unsymmetrsich (kausale) Form annimmst, eigentlich.

 

[starling]

beginnt mit leisen hohen Frequenzen dann kommen mehr tiefe Frequenzen dazu ->gipfelt im lautesten Punkt mit noch mehr Frequenzen und dann hört er genauso auf wie er anfing

Schau Dir das Bild von Swissdoc an - die tiefen und hohen Frequenzen sind überall gleich
Nur die Wellenform die aus der Überlagerung entsteht, sieht so aus als ob sich etwas ändern würde.

In seinem Beispiel ein Rechteck.
Und diese Wellenform hängt auch von den Phasen ab. Wenn Du die tiefe Welle verschiebst, hast Du kein Rechteck mehr.

 

[weird fish]

Vielleicht etwas OT, aber hier sieht man einen 5ms Puls auf verschiedene Arten gefiltert (siehe Anhang). Von oben nach unten:

- original Puls
- FIR-Filter (linear phase) 1kHz, 96dB/Oct, Latenzkompensiert
- IIR-Filter 1kHz LPF, 96dB/Oct *
- FIR-Filter (linear phase) 100Hz, 96dB/Oct, Latenzkompensiert
- IIR-Filter 100Hz, 96dB/Oct *
- FIR-Filter (linear phase) 50Hz, 6dB/Oct, Latenzkompensiert
- IIR-Filter 50Hz, 6dB/Oct

Es scheint so, als dass beim FIR-Filter die Wirkung (dieses so genannte Preringing) der Ursache vorweg geht, was ja eigentlich in der Praxis nicht möglich ist. In Wahrheit hat aber ein FIR-Filter eine gewisse Latenz, die notwendig ist, damit der Algorithmus weis was in Zukunt passiert, damit er dieses Preringing überhaupt erzeugen kann. In der DAW wird diese Latenz dann wieder kompensiert, wodurch es wirkt, als könnte der Algorithmus hellsehen. Dieses Ringing ist notwenig, weil die Obertöne fehlen, die für ein "scharfen Knick" in der Amplitude erforderlich wären. Also schaukelt es sich langsam hoch (wie ein Kind auf der Schaukel) (man beachte dazu auch den Unterschied 6dB/oct vs. 96dB/oct). Ein konventionelles Filter, hat weder Latenz noch dieses Preringing-Problem, dafür allerdings ein Postringing, das im schlimmsten Fall nie aufhört (deswegen Infinit Impulse Response -> siehe Selbstoszillation eines Synthesizer-Filters) und es verschmiert die Phasen der enthaltenen Teilschwingungen sowohl im Pass- wie auch im Sperrband.

Ich hoffe, ich konnte noch ein paar Klarheiten beseitigen

 

[betadecay]

Für mich sieht das eher nach einem Wavelet aus: https://de.wikipedia.org/wiki/Wavelet

Hier https://de.wikipedia.org/wiki/Wavelet#S ... rarbeitung heisst es "Die Waveletmaske entspricht der Impulsantwort eines Bandpassfilters [...]"

Kann es sein, das es weniger um eine Pulswelle als eher um eine Impulsantwort geht?

Vielleicht könnten die Physiker hier im Forum dazu erhellendes beitragen...