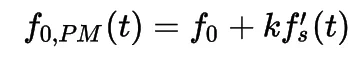MvKeinen
||||||||||
Ich wollte jetzt mal grundsätzlich etwas für mich klären, wo ich nur Vermutungen habe und in Gesprächen manchmal an Grenzen stoße:
Folgendes ist eher nur so halbwissen:
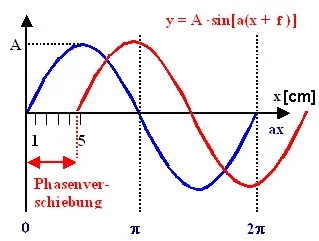
Diese Phase wäre dann eine Rampe (steigender Sägezahn) von 0° - 360°.
Bei digital: Hier wird abhängig von der Frequenz und der Samplingrate ein sehr kleiner Incrementwert errechnet der bei jedem sampling Clock zum vorherigen Phasenwert addiert wird. Bei dem Wert 1 wird das ganze auf 0 herabgesetzt und der Vorgang wiederholt sich. -> Saw von 0 bis 1
Bei analog: Da gibt es Oscs mit Saw oder Tri -Kern. Ich denke da wird etwas aufgeladen und per comparator bei einer bestimmten Spannung entweder komplett (Sawkern) oder progressiv (Trikern) entladen.
Bei beiden Technologien werden dann aus dieser Grundwellenform per Waveshaping alle anderen Wellenformen generiert.
Wenn jetzt diese Phase moduliert wird, wird ihre Amplitude moduliert (es wird der Zeitpunkt innerhalb des zyklischen Vorganges verschoben) allerdings gelten für das Ergebnis immernoch die "umklapp" Regeln, so dass auch ein negatives Delay möglich sein muss.
oder ist das eher dann doch nur ein Delay???
Phase = Phasenwinkel (wiki): Der Phasenwinkel oder die Phase gibt die aktuelle Position im Ablauf eines periodischen Vorgangs an.
Folgendes ist eher nur so halbwissen:
Diese Phase wäre dann eine Rampe (steigender Sägezahn) von 0° - 360°.
Bei digital: Hier wird abhängig von der Frequenz und der Samplingrate ein sehr kleiner Incrementwert errechnet der bei jedem sampling Clock zum vorherigen Phasenwert addiert wird. Bei dem Wert 1 wird das ganze auf 0 herabgesetzt und der Vorgang wiederholt sich. -> Saw von 0 bis 1
Bei analog: Da gibt es Oscs mit Saw oder Tri -Kern. Ich denke da wird etwas aufgeladen und per comparator bei einer bestimmten Spannung entweder komplett (Sawkern) oder progressiv (Trikern) entladen.
Bei beiden Technologien werden dann aus dieser Grundwellenform per Waveshaping alle anderen Wellenformen generiert.
Wenn jetzt diese Phase moduliert wird, wird ihre Amplitude moduliert (es wird der Zeitpunkt innerhalb des zyklischen Vorganges verschoben) allerdings gelten für das Ergebnis immernoch die "umklapp" Regeln, so dass auch ein negatives Delay möglich sein muss.
oder ist das eher dann doch nur ein Delay???