Pure Data Experiment: Berechnung Intensität Obertöne

[_thomas_]

Aktuell sitze ich an einem kleinen Harmonie-Experiment basierend auf dem Lambdoma. Zur Berechnung der Harmonien nutze ich der Einfachheit halber Pure Data.

Das ist jetzt aber gerade nicht der Punkt. Zum Lambdoma komme ich vielleicht auch noch, sollte ich daraus eine sinnvolle Anwendung entwickeln können.

Vorweg: In der Musiktheorie kenne ich mit nur rudimentär aus. Kann sein, dass meine Terminologie nicht so wirklich passt.

Aber mal in Kürze: Das Lambdoma berechnet Harmonien. Jeder der sich ein wenig mit Tonleitern beschäftigt hat weiß, dass es hier eigentlich nur um Mathematik und Relationen geht. Hält man sich daran hört es sich alles "harmonisch" an. So hat man z. B. von einer Oktave zur nächsten immer die doppelte Frequenz: C1 => C2 = 32,7032 Hz => 65,4064 Hz. Und so stehen alle Töne einer Tonleiter in einer Relation zueinander. Und lassen sich somit berechnen. Das Lambdoma ist einfach eine Matrix oder auch ein Diagramm welches diese Relationen abbildet.



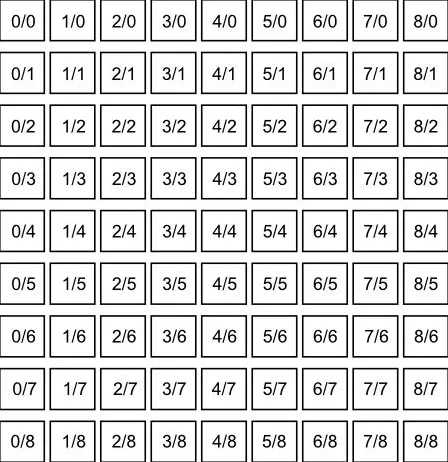
Aber wie gesagt: Das ist nur der Hintergrund, darum soll es gerade gar nicht gehen.

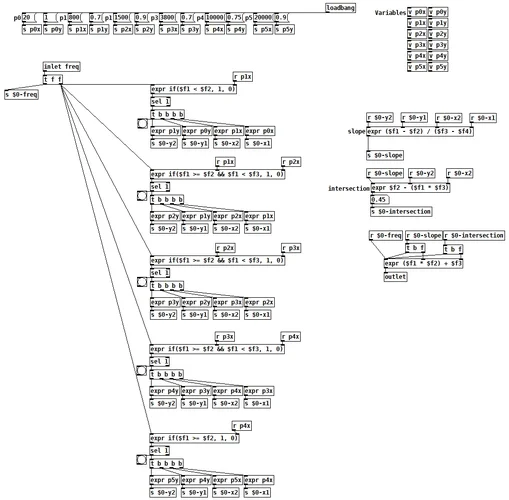
Hier in den unteren Anzeigen steht links die Basisfrequenz und dann folgen drei Relationen, einstellbar mit den Werten im roten Rahmen. Man kann die Relationen einstellen wie man will, es wird sich immer "harmonisch" anhören. So weit, so gut. An jeder Relation hängt ein Oszillator dem ich die berechnete Frequenz übergebe.



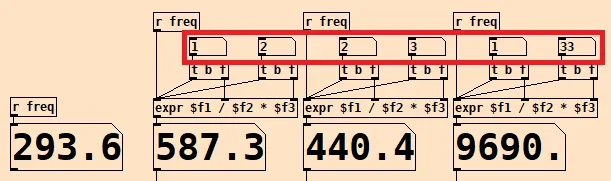
Hier also vier Oszillatoren.

Jetzt komme ich zum Punkt: Es geht mir um die Intensität/Lautstärke der einzelnen Oszillatoren im Mix.



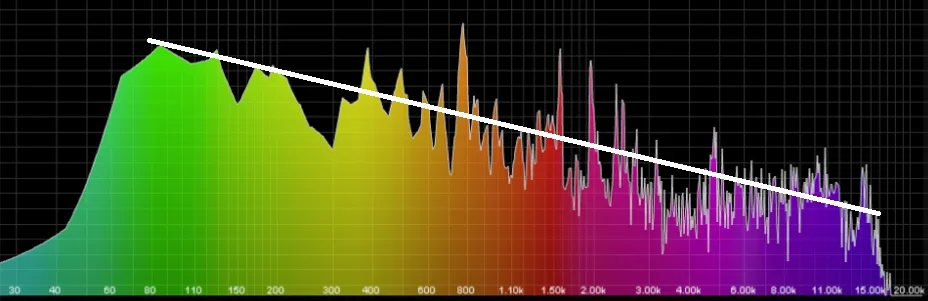
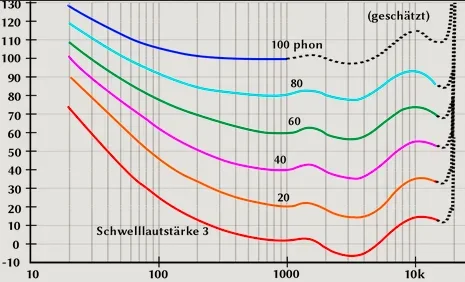
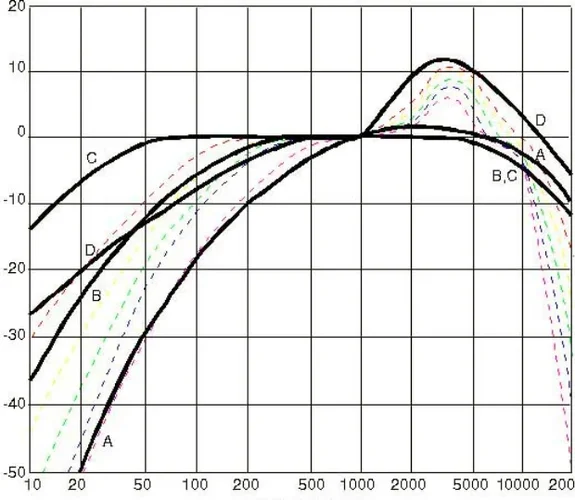
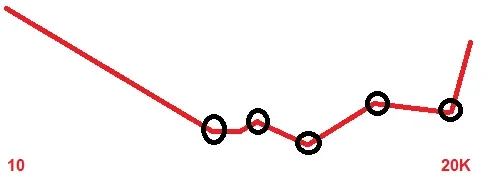
Was ich hier im Forum gelernt habe: Je höher die Frequenz, desto besser die Wahrnehmung. Haben die Oszillatoren alle dieselbe Lautstärke hört sich das doof an. Daher ist es auch sinnvoll höhere Frequenzen leiser zu machen als niedrige. Auch das ist ja erstmal einfach: Ich denke mir hier eine Lautstärkelinie wie oben im Spektrum und setze die Frequenz in Relation zur Lautstärke. Darauf stelle ich dann die Lautstärke des Oszillators ein. Fertig. Das ist natürlich irgendwo stark idealisiert und hat (wie man am Spektrum ja auch erkennen kann) mit der Realität nicht unbedingt was zu tun.

Eine spezielle Frage dazu habe ich eigentlich nicht. Aber vielleicht habt ihr Meinungen dazu wie man es intelligenter, optimaler oder was auch immer machen könnte.

 

[einseinsnull]

Vorweg: In der Musiktheorie kenne ich mit nur rudimentär aus. Kann sein, dass meine Terminologie nicht so wirklich passt.

richtig ist, was verstanden wird. bastel your own musiktheorie.

Jeder der sich ein wenig mit Tonleitern beschäftigt hat weiß, dass es hier eigentlich nur um Mathematik und Relationen geht.

manchmal ja, manchmal nein.

eine wie auch immer geartete reine stimmung, so wie in dieser chart, zu benutzen wenn man #irgendwasmitadditiv macht, ist aber absolut zielführend.

Was ich hier im Forum gelernt habe: Je höher die Frequenz, desto besser die Wahrnehmung.

nicht wirklich, eher sind die mitten am lautesten.

und leider ist es noch komplizierter, und es reicht nicht ganz aus nur das verhältnis von frequenz und lautheitsempfinden zu berücksichtigen, da sich das empfinden stark ändern kann, wenn nicht nur reine töne (und die solo und abwechselnd) spielen.

auch die harmonien und die transienten haben eine wirkung auf das lautheitsempfinden einzelner schallereignisse.

letztlich hängt das empfinden für den relativen unterschied auch von der gesamtlautstärke ab. das gilt bedingt für die schmerzgrenze, aber vor allem gilt das für die wahrnehmungsschwelle.

wie oben im Spektrum und setze die Frequenz in Relation zur Lautstärke. Darauf stelle ich dann die Lautstärke des Oszillators ein. Fertig.

es ist in jedem fall sinnvoller solche experimente zu machen als sie nicht zu machen.

erwarte aber nicht zuviel davon.

Eine spezielle Frage dazu habe ich eigentlich nicht. Aber vielleicht habt ihr Meinungen dazu wie man es intelligenter, optimaler oder was auch immer machen könnte.

ich habe für eine performance letztes jahr eine anpassung an eine loudness kurve in einen solchen additiven synth miteingebaut (neben diversen anderen kurven) und musste feststellen, dass der effekt letztlich durch die raummoden eh wieder verpfuscht wird. sowas funktioniert meist nur im labor oder mit dem 1000 euro kopfhörer.

ein versuch ist es aber immer wert. dabei steht dann die frage im vordergrund ob es überhaupt sinn macht das ans gehör anzugleichen, was ja eigentlich seine eigene wahrnehmung bereits so kennt wie sie halt schon immer war.

wenn das gehirn es gewohnt ist, dass bei sweeps von reinen tönen oder harmonischen - oder es könnte auch das weiße rauschen sein - bestimmte frequenzbereiche als weniger laut empfunden werden als andere, dann stellt das ja auch eine form eines normalzustands dar, auf die sich die veränderte, vermeintlich angepasste kurve dann bezieht.

welches davon ist der ausgangspunkt, das lineare - und welches davon ist moduliert/verzerrt...?

 

[marco93]

Sorry für offtipc, aber wie lange dauert es etwa, bis man mit PD Musik machen kann, wenn man bei 0 angfängt.

 

[_thomas_]

wenn man bei 0 angfängt

Die Basics hat man recht schnell drauf. Inklusive Installation sollte es möglich sein in 30 Minuten einen ersten Sound zu erzeugen.

Fragen dazu besser hier: https://www.sequencer.de/synthesizer/threads/pure-data-organelle-max-msp-q-a.160355/

Wir unterstützen gerne.

manchmal ja, manchmal nein.

Als nächstes mache ich dann vielleicht irgendwas mit Mikrotonal.

eher sind die mitten am lautesten

Also die Mitten etwas dezimieren. Das kann ich ja einfach mal testen und eine Gewichtung einbauen. Den Rest deiner Anmerkungen ignoriere ich vorerst besser.

erwarte aber nicht zuviel davon

Ich erwarte erstmal gar nichts. Ob das irgendwo hinführt kann ich gar nicht sagen. Die meisten meiner "Experimente" in der Klangerzeugung waren mehr oder weniger Fails. Nur an Erfahrung bin reicher geworden. Umsonst war also nichts.

 

[einseinsnull]

Also die Mitten etwas dezimieren. Das kann ich ja einfach mal testen und eine Gewichtung einbauen. Den Rest deiner Anmerkungen ignoriere ich vorerst besser.

es ist insofern weniger kompliziert als wie du denkst, weil das, was ich oben noch an zusätzlichem theoriegedöns ergänzt habe letztlich bedeutet, dass man das eh nicht perfekt hinbekommen kann.

über lautstärkewahrnehmung werden sich die wissenschaftler noch 100 jahre streiten und es kommt immer mal wieder etwas neues raus, was es zum industriestandard schafft.

wenn du die dazu üblichen und etablierten kurven benutzt gibt es dafür vor allem keine idealisierte formel um diese zu berechnen, ich habe mir da auch schon einen wolf gesucht und letztlich gibt es nur fucking tabellen, die man sich selbst irgendwie herbei-runden muss.

ich rate dazu, das alles in signal zu machen und die kurven in einen lookup table zu schreiben. (hertz rein, linear gain raus), denn der spass fängt erst richtig an, wenn du das zeug auch vernünftig in der frequenz modulieren kannst.
dabei kannst du direkt auch das bandlimiting mit reinrechnen, vor allem am low end musst du eh von der wahrnehmung abweichen und einen "hochpassfilter" rein machen, der je nach lautsprecher set variiert.

 

[einseinsnull]

du versuchst das hier mithilfe frei erfundener formeln nachzubilden, und zwar für ca. ~70db:



oder der einfachheit halber erst mal eine davon:




dann wandelst du db in linear um, stellst das ganze auf den kopf und schreibst es in einen buffer.

um es zu invertieren musst du vorher das "unendlich" wegbekommen, indem du z.b. bei -144 clippst.

 

[_thomas_]

du versuchst das hier mithilfe frei erfundener formeln nachzubilden

Sagen wir: stark vereinfacht, näherungsweise aber erstmal okay.

Erstmal danke für deine Infos. Das über die von dir gezeigten Kurven zu berechnen (näherungsweise mit sagen wir 100 oder 200 Punkten und dann interpoliert) ist ja prinzipiell auch kein Problem. Aber aufwändig da die sich ja auch noch je nach Höhe des Schallpegels verändern. Ich werde erstmal meinen lineraren und vollkommen unrealistischen Ansatz fortsetzen und ein paar Parameter hinzufügen um die Steigungen für bestimmte Bereiche anzupassen.



Bevor ich anfange das total sophisticated zu gestalten. Die Wahrscheinlichkeit ist halt hoch, dass dabei nichts Sinnvolles herauskommt. Da reicht mir die Näherung erstmal aus.

 

[_thomas_]

So schnell vergeht ein Freitagnachmittag.

Ich ermittle

• die richtige lineare Funktion anhand der Frequenz (inlet freq), also sowas wie eine Frequenzweiche
• sende die entsprechenden Punkte p1 und p2 der gefunden Funktion an die Berechnung der Steigung (slope)
• sende die Steigung an die Berechnung des Schnittpunkts
• und ermittle dann mein y (Lautstärke) basierend auf x (Frequenz)

Funktioniert tadellos. Natürlich muss ich hier mit y-Werten zwischen 0 und 1 arbeiten weil das on PD halt so ist. Aktuell stehen auch nur Testwerte drin. Da muss ich also noch schauen ob ich die Wahrnehmungskurve nicht auch irgendwo mit konkreten Daten frequenz/db oder wenigstens frequenz/phon irgendwo finde. Ansonsten bleibt mir nur das mit dem Gehör so halbwegs einzustellen. Und wie viel db 0 und 1 sind weiß ich ja eigentlich auch nicht. 1 wird wahrscheinlich 0 db sein. Die vier Punkte kann ich sogar noch per Inlet zur Verfügung stellen. Dann ist das sogar modulierbar. Punkt 0 ist alles unterhalb von 10 Hz, Punkt 6 alles oberhalb von 20 kHz.

Den Patch selbst muss ich noch optimieren. Aber erstmal läuft das so. Ich hoffe, dass das jetzt doch zu etwas führt. Wo so viel Zeit drin steckt...

 

[einseinsnull]

richtig, in der ersten version machst du einfach 10 oder 50 punkte und interpolierst "irgendwie".

passende funktionen dazu finden kann später ganz gut gehen, indem man einfach das graphische ergebnis mit den augen abgleicht.

generell ist die "rückwärtssuche" nach funktionen für bestimmte ergebnisse leider nicht immer ganz einfach, aber mit trial und error kommt man auch irgendwann hin.

ich persönlich würde die schwarz-weiß bildchen ignorieren. diese bel/sone/brt welt ist für unsere zwecke suboptimal. die komplizierter aussehenden kurven wurden von psychologen mit testhörern erarbeitet, die simplen von mathematikern nur angenommen.

was die werte aus den tabellen angeht, die sind selbst in in den papers so rudimentär, dass es besser ist einfach das wikipedia bild zu nehmen und das in einem bildbearbeitungsprogramm mit einem lineal auszumessen.

Und wie viel db 0 und 1 sind weiß ich ja eigentlich auch nicht

expr (pow(10.\, $f1*0.05))*($f1!=-90.)

(90 entspricht 16 bit audio, für >24 könnte man dann -144 nehmen. weil mit unendlich kann man schlecht multiplizieren.)

 

[_thomas_]

Wenn du zwei Punkte hast ist das linear ja recht einfach.

y = mx + b

y = Lautstärke
x = Frequenz

Wenn die Auflösung hoch genug ist (also genügend Punkte) dann ist das schon ausreichend finde ich. Wir wollen es ja nicht übertreiben...

 

[einseinsnull]

und immer mit mittlerer lautstärke abhören, sonst funktionierst es nicht.

ein guter test ist: um 6 db zu erhöhen und mal zu schauen, ob es sich genau doppelt so laut anfühlt. bei 1000 hertz tut es das per definitionem...

Wenn du zwei Punkte hast ist das linear ja recht einfach

oder einen counter laufen lassen und die quantisiert vorliegenden werte durch ein [slide] oder onepole filter schicken.

 

[einseinsnull]

so, ich muss jetzt leider eis essen gehen.

 

[_thomas_]

Alles klar, und ich muss duschen gehen. Die Woche ist schon wieder um.