Digitale Synthesizer
3. Synthesetechniken
3.3 Weitere Algorithmen
- physical modeling, fm-synthese, etc.
QUICKLINKS tutorial sektion: einfache erklärung fm
fm synthese (mehr infos) fm
find a complete "how to make a bass with FM" tutorial here / Tutorial für FM Bass Sounds hier..
Eine absolut vollständige Beschreibung aller existenten Synthesen und Baugruppen ist (in diesem Rahmen) nicht möglich, daher wurde die hier vorliegende Art dieser Arbeit gewählt. Für weitere Informationen empfehle ich einen Blick in die Fachliteratur und Experimentieren mit den Geräten und Programmen, insbesondere für grundlegende Themen wie Filterbau, etc...
Eine Technik, die nicht unerwähnt sein darf, ist die FM-Synthese (Frequenzmodulation), welche vor allem in Yamahas DX Serie, ab 1983, u.a. in Form des wohlbekannten "DX7" Anwendung fand. Hier sind Oszillatoren (bei Yamaha "Operator" genannt), in einer bestimmten Weise miteinander verknüpft (Yamaha nannte dies "Algorithm".
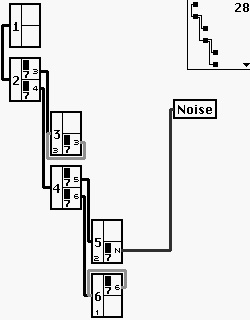
Die DX und TG / SY serie bis zum FS1R (english)). Die Anzahl der Oszillatoren war bei den meisten Geräten auf sechs oder vier pro Stimme festgelegt. Jeder Oszillator hat eine Lautstärkenhüllkurve und kann in ihrem Frequenzverhältnis zu den anderen Oszillatoren jeweils eingestellt werden, da dies entscheidend für die Klangformung ist: Der unterste der Oszillatoren "in einem Strang" (Algorithm) ist der sogenannte Träger, der durch seine Hüllkurve ein- und ausblendbar ist und für den Lautstärkenverlauf sorgt. Der nächste Oszillator, der den Träger in seiner Frequenz steuert, der Modulator, kann nun durch seine Hüllkurve (obwohl sie, nach wie vor, die Lautstärke dieses Modulators steuert) den Klang verändern, da er ja die Frequenz des Trägers steuert, mit der Intensität des aktuellen Hüllkurvenpegels. Nun kann auch der nächste Oszillator den modulierenden Oszillator abermals modulieren und durch seine Hüllkurve für eine komplexere dynamische Klangsteuerung sorgen. Sechs nebeneinander liegende (parallele) Träger sind genauso möglich (wie bei einer Zugriegelorgel einfach 6 ein- und ausblendbare Töne einer festen Frequenz / keine FM), wie auch sechs sich gegenseitig modulierende, lediglich festgelegt. Durch den "Algorithm", ein Schaltbild, welches sich auswählen und sogar im Falle der TG /SY (77 und 99) - Modelle frei definieren läßt, kann man alle parallelen und seriellen Kombinationen ausschöpfen.
Die mathematischen Grundlagen dieser und anderer Synthesetechniken sowie der Interpolation sind sehr weitreichend und können unter anderem im "Taschenbuch mathematischer Formeln" von Dr. Ing. Hans-Jochen Bartsch, ISBN 3-343-00876-1, Fachbuchverlag Leipzig - Köln ausführlich untersucht werden.
Die additive Synthese findet zur Zeit neue Beliebtheit in Form der Kawai K5000-Serie, dem "Emulator IV" (bedingt) und Computersystemen wie etwa "Kyma" und "Generator".. Hier werden eine Anzahl von meist 64 oder 128 Obertönen (Teiltönen) mit je einer Hüllkurve versehen(!) und einzeln editiert(!). Die Zusammensetzung dieser Teiltöne (in "Reintheorie" Sinusschwingungen der x-ten Vielfachen des Grundtons!) ergibt den komplexen Gesamtklang und erhält seinen Namen aufgrund der Addition der Einzelteiltöne. Wenn man eine dreidimensionale Landschaft (entsprechend den Achsen: Amplitude, Frequenz und Zeit) aufgezeichnet hat, so bekommt man einen Eindruck dieser Synthese: Die Amplituden über der Zeit (ein zeitlicher Hüllkurvenverlauf der Amplitude einer Frequenz / die zweite Dimension im Gebirge) sind einzelne Scheiben in diesem Gebirge. Jede Scheibe steuert die Lautstärke eines Oszillators einer bestimmten Frequenz, der dritten Dimension in diesem Gebirge entsprechend. Nachteile sind: sehr viele Parameter, denn, genaugenommen, müssen noch diese Dinge geschaffen werden:-
Phasensteuerungshüllkurven-
Frequenzhüllkurven
- Gegen "unendlich" viele Oszillatoren, auch mit nicht ganzzahligen Frequenzen
- Jemand, der dies überschauen kann
In der Praxis werden Makros (Ein Befehl für viele Einzeloperationen) benutzt, dafür keine der genannten letzten Punkte realisiert (bisher). Kawai versucht es mit einem Spektrum, welches als "Filter" vom aktuellen Spektrum subtrahiert wird und beweglich ist (frequenzmäßig), dadurch ist ein quasi "charakteristikprogrammierbares" Filter entstanden. Mathematisch ist hier eine (Fourier-)Reihe der einzelnen Sinusfunktionen pro Teilton zu bearbeiten, dessen Umfang ebenfalls enorm ist und durch externe, o.a. Literatur eingesehen werden kann. Der Anwender bekommt natürlich das mathematische Innenleben seiner Geräte nicht mit. -Einen kleinen Eindruck dessen bekommt man jedoch bei Ansicht der Filterkonstruktion (Kapitel 3.1.1.). Korgs Prophecy gab man gleich diese Synthesen mit: FM, subtraktive, VPM (Phasenmodulation), Sync./Ring/Cross, Waveshaping etc.. und eine Entwicklung der neueren Zeit zeichnet sich neben vielen subtraktiven und additiven Mischarten der Klangerzeugung ab: das "physical modelling". Aufgrund der physikalischen Grundlagen eines akustischen Instrumentes wird ein Algorithmus angewendet, der sich oft auch aus der "real üblichen" Parameterisierung entfernt, jedoch an die physikalisch-mathematischen Grundlagen der Originalinstrumente angelehnt ist. So kann aus dem physikalischen Algorithmus ("Modell") einer gezupften Saite und einer Luftsäulenschwingung (mit Resonanzraum), aus einem "Flötenmodell" eine "gestrichene Flöte" werden, u.ä. Die so gewonnenen Klänge haben oft ein Höchstmaß an Authentizität bei "wenigen" Parametern, denn die Rechenvorschrift ist ja eine genaue naturwissenschaftliche / mathematische Beschreibung des akustischen Instrumentes. Vertreter dieser Gerätegeneration sind Yamahas VL1, VP1 und VP70m (gegen die die Prophecy-Modelle eher Versuche sind) etc..
Das Selberschaffen dieser Algorithmen erfordert also entsprechende fundierte Kenntnisse im akkustisch / physikalischen Bereich. Man benutzt die vorgegebenen Parameter.
Natürlich ist bei allen Syntheseverfahren in realen Systemen immer nur eine "Teil-Authenzität" anzunehmen, denn das "Original" kann aufgrund seiner physikalischen Existenz nicht zu 100% realisiert werden, jedoch ist (wie generell in der Synthesizertechnik) auch nicht der Ersatz der traditionellen Instrumente das Ziel, allenfalls deren "Simulation" und Verbesserung, um eine Musik Produktion schneller und unkomplizierter zu realisieren. (Bei entsprechender Spielweise kann ein "Modell" trotzdem sehr "echt" klingen.) Die Stärken der synthetischen Klangerzeugung sind neue, vorher "ungehörte" Klänge. Beim physical modelling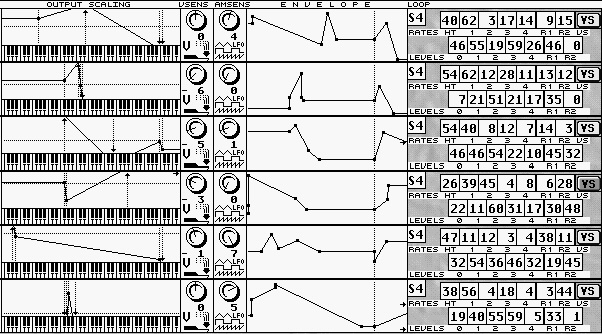 
ist man jedoch sehr gefordert, wenn man dies einfach "heraushören" will. Nichtsdestotrotz ist das wirklich Interessante dieser Technik, die "Grenzbereiche" der Modelle zu finden und sie für ein neues virtuelles akustisches Instrument zu verwenden, das wohl real nie gebaut werden wird.
Dies sind: Algorithmus mit 2 Trägern, der untere Strang wird moduliert. Op.2 von Op.4 und Op.6 etc.. (rechts) und ein Ausschnitt aus dem Hüllkurventeil sowie der Keyboardskalierung eines Yamaha TG77 (links)
find a complete "how to make a bass with FM" tutorial here / Tutorial für FM Bass Sounds hier..
Fs1R Algo-Struktur:
vergrößern = draufklicken..
