Synthesizer-Diplom (Synthesetechniken 2 – Subtraktive Synthese)
Digitale Synthesizer
3. Synthesetechniken
3.1 Subtraktive Synthese / Sampling
3.1.1 Baugruppen (zu DIGITALEN filtern weiter unten) zunächst basiswissen:
Die digitalen Komponenten der subtraktiven Synthese sind mit der gleichen Zielsetzung der entsprechenden Analogbausteine konstruiert worden: Ein oder mehrere Oszillator/en, die klangerzeugenden Teile des Systems, welche meist ein obertonreiches Spektrum besitzen, durchlaufen ein Filter, das einen Teil dieser Obertöne dynamisch -durch Herausfiltern bestimmter Teiltöne- verändert. Der klassische Aufbau besagt die Zusammenmischung der Oszillatoren vor dem Filter in einer Mischstufe, was auch heute die Regel ist. Nachgeschaltet ist ein Vertärker, der dynamisch kontrolliert wird und eine Panoramaeinheit, die die Verteilung zwischen linker und rechter Seite reguliert. So hat man die drei Blöcke aus der Analogwelt auch hier: Oszillatorteil für Tonerzeugung und Tonhöhe, Filterteil für Klang (beziehungsweise Obertonänderungen) und Verstärker- mit Panoramamodulteil für die Lautstärkenkontrolle. Der dynamische Verlauf dieser „Teile“ ist dabei der wichtige Faktor. Modulation heißt, eine Steuerung eines Parameters eines Moduls oder Baugruppe durch einen anderen beliebigen oder „festverdrahteten“ Parameter, der auch auf einem anderen Modul erzeugt worden sein kann (auch extern durch Schnittstellen.. u.a.).
Die wichtigsten Grundbausteine zur Steuerung der Hauptbauteile aus digitaler Sichtweise:
Hüllkurven („Envelope“): Eine Liste von Pegeln, die in einer bestimmten, zugehörigen Zeit erreicht werden. Je nach Pegelstand wird ein Steuerwert dementsprechend übergeben (an den zu modulierenden Parameter). Alle resultierenden Zwischenstände sind durch Interpolation immer vorhanden.
Einfachere Formen verwenden die gebräuchlichste Struktur „ADSR“ (Attack, Decay, Sustain, Release), der Analogsysteme: Nach einer Zeit „Attack“ wird das Steuersignal von Null- auf Maximalpegel gebracht, danach (innerhalb der Zeit „Decay“) erfolgt der Rückfall auf den „Sustain“-Pegel. Die „Release“-Zeit gibt anschließend die Zeit an, die bis zum Erreichen des Nullpegels vergeht (in der Regel nach Loslassen der Klaviaturtaste).
Selbstverständlich gibt es hier noch einige andere Arten, die aber demselben Zweck dienen: Mit Hüllkurven können (Steuerungs-) Verläufe automatisiert werden. Für den Lautstärke- und Filterteil steht meist standardmäßig je eine Hüllkurve zur Verfügung, sie werden dann durch (Klaviatur-) Tastendruck aktiviert („getriggert“) und gestartet.
LFOs: Im Gegensatz zu den normalen Audiooszillatoren (Schwingungsgeneratoren), schwingen diese „Low Frequency Oscillator“, also „niederfrequente Oszillatoren“ genannten Modulationsquellen im unteren Frequenzbereich mit regelbarer Frequenz. Dies würde weniger Rechenleistung als ein dementsprechender (im Hörbereich arbeitender) Oszillator benötigen. Der abgedeckte Frequenzbereich ist etwa zwischen 0,2 bis 30 Hz festgelegt, kann aber auch bei einigen Geräten wesentlich erweitert worden sein und in den Audiobereich hineingehen oder ihn ganz abdecken (für „FM-Synthese“ notwendig, s.u.)! Auch hier sind verschiedene Wellenformen im Angebot. Eine immer häufiger in Instrumenten anzutreffende „Minihüllkurve“ kann den LFO-Pegel ein- und ausblenden. Etwas wie z.B. „einschwingendes“ und „abklingendes“ Vibrato läßt sich so einfach simulieren.
Tracking: Dient der Anpassung von Klaviatur (Keyboard) und Controllern (MIDI-Pegellieferanten, die zur Echtzeitmodulation herangezogen werden) und gibt an, wie stark sich ein Parameter durch einen anderen verändern soll und wie (in welchem Verhältnis) er sich ändert, wenn sich der ursprüngliche Parameter ändert („Skalierung“). Häufig verwendet ist das „Keytracking“, je höher die gespielte Note (o.a. Parameter) auf der Klaviatur ist, desto mehr soll ein Filter öffnen oder bestimmte Hüllkurvenparameter verändert werden, welche dann Filter und Lautstärke steuern; für Pianoklänge ist dies dringend nötig!
Andere Verwendungsformen sind: Anschlagstärkekennlinien, Klaviaturskalierungen, etc…
Für die Oszillatorensektion gibt es ebenfalls vielfältige Oberton-Variationsmöglichkeiten wie:-
Synchronisation eines Oszillators mit einem anderen, also das Erzwingen eines erneuten Wellenformstartes des synchronisierten Oszillators, gesteuert durch den Wellenverlauf (Periodendauer) des ersten (meist bei Nulldurchgang mit steigender Tendenz).-
Waveshaping: Änderung der Wellensymmetrie oder Verformung der Welle nach bestimmten Gesetzen (wie digitale Übersteuerung „clipping“…etc…) –
Frequenzmodulation (FM): In digitalen Geräten oft durch die Möglichkeit gegeben, durch einen Audiooszillator die Frequenz des nächsten zu modulieren. Hier können „metallische“ und „glockige“ Klänge leicht realisiert werden. Entscheidend ist das Verhältnis der Frequenzen.-
Amplitudenmodulation (AM): dito, jedoch wird die Lautstärke des nächsten Oszillators gesteuert.-
Phasensteuerung- / Modulation: Die Startphase / Phasenlage eines (mehrerer) Oszillators/en kann hier gesteuert werden, (z.B. durch den jeweils anderen Oszillator.)-
Die Oszillatoren haben eine Technik der kontinuierlichen Wellenformveränderung durch mathematische Funktionen oder Wellenformtabellen-
Die Oszillatoren geben Samples wieder, also gespeicherte „Aufnahmen“ von Klängen.-
Ringmodulation: Errechnet aus den Eingangsfrequenzen zweier Oszillatoren Summe und Differenz (aus „200Hz“ und „150Hz“ werden „350Hz“ und „50Hz“). Diese resultierenden Frequenzen sind keine Vielfachen der Eingangsfrequenzen, da sie „unharmonische“ Klänge erzeugen sollen. Diese Einrichtung kann auch als AM benutzt werden (Zweiter Oszillator ist frequenzmäßig unterhalb des Hörbereichs).
Die Filtersektion ist ein vielgeschätzter Teil und ein erst in letzterer Zeit klanglich ernstnehmbar und konkurrenzfähig zu analogen Pendants gewordenen Hauptbestandteile, denn es gilt nicht nur, einfach die folgenden Typen zu generieren, sondern auch die typischen Verzerrungen, Resonanzen und Rückkopplungen der analogen Vorbilder zu simulieren und zu verbessern. Dabei ist das Filter auch der eigentliche „Synthesen-Namensgeber“, denn er sorgt für das „Subtrahieren“, das „Abziehen“ der Teiltöne im Frequenz-Spektrum (Amplituden aufgetragen zu den ganzzahligen x-fachen der Grundfrequenz).
Eine Kurzerklärung der synthesizertypischen Filterarten folgt auf der nächsten Seite… (Rechts daneben findet man eine vereinfachte und stilisierte Prinzip Skizze mit „Resonanzbuckel“ im LPF & HPF. Sie zeigt den Obertongehalt im Frequenzverlauf).
LPF: Low Pass Filter (Tiefpaß): Sperrt ab einer
Eckfrequenz mit einer bestimmten Steilheit und
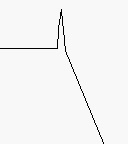
Resonanz (Erhöhung um die Eckfrequenz herum).
HPF: High Pass Filter (Hochpaß): dito, allerdings
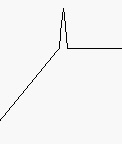
sperrt er unterhalb der Eckfrequenz…
BRF: Band Reject Filter („Notch“ / Kerbfilter):
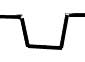
Sperrt von einer unteren Frequenz bis zu einer oberen Frequenz
(Bandbreite) mit einer Flankensteilheit (x dB/Oktave).
(bild zerstört).. entspricht etwa umgekehrtem
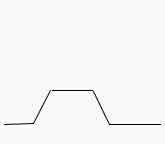
BPF: Band Pass Filter (Bandpaß): Entspricht einer
Kombination aus LPF und HPF, dem „Gegenteil“ von BRF: Läßt den Bereich zwischen zwei Frequenzen unter Berücksichtigung der Flankensteilheit durch.
Alle Filtertypen können einen „Resonanzbuckel“ bekommen, der den typisch „elektronischen“ Klang ausmacht. Diese sind Vertärkungen/ Betonungen um die Eckfrequenz herum. Die Resonanz ist bei guten Filtermodellen bis zur Selbstoszillation bringbar, und der kritische Punkt bei Vergleichen ist der Bereich „kurz vor Selbstoszillation“, denn hier sind mathematische Verfahren der „chaotischen“ Verzerrungssimulation rechenintensiv und schwierig zu programmieren / algorithmisieren (d.h. „zu mathematisieren“). Ein zweiter Punkt ist, wie stark die Resonanz den Klang „ausdünnt“ (Gegenmaßnahme: „Rückkopplung“ auf den Eingang / Ausgangsparameter beeinflussen aktuelle Berechnung).
Auch digitale vollparametrische Equalizer oder ganz spezielle Filterdesigns wie in E-mu´s Z-Plane – Synthese sind willkommene Klangdesign-Alternativen; machbar durch die Kombination verschiedener Filtertypen, die parallel oder seriell verschaltet werden.
Die Steilheit der Filter wird durch Anzahl der „Pole“ erkennbar (pro Pol: 6 dB pro Oktave Dämpfung). Die gebräuchlichste ist: 4 Pol LPF, also ein 24 dB/Oktave – Tiefpaß-Filter. Die E-mu Filtermodelle haben 14-polige Kombinationen aus obigen Filtertypen, wodurch auch „Kammfilter“ (mehrere regelmäßige „Kerben“) und Überblendungen zwischen Filterarten („Filtermorphing“) etc.. möglich werden. Die sogenannten APF (Allpaßfilter) kommen seltener zum Einsatz, sie haben keine „Filterwirkung“, aber eine Phasenveränderung zur Folge, wie alle anderen Typen ebenfalls, was zusätzlich die oben erwähnte Errechnung erschweren kann.
Zum Abschluß der subtraktiven Systeme die generelle Funktion des digitalen Filters
WIE FUNKTIONIEREN DENN NUN DIGITALE FILTER?
Wie bei den meisten wichtigen Synthesizerbauteilen halten die Firmen aus verständlichen konkurrenz- / markttechnischen Gründen ihre genauen Filteralgorithmen geheim, daher kann ich hier (wie auch auf andere genaue Techniken zutreffend) nur prinzipielle Lösungen geben, die in den fertigen Produkten komplizierter und besser sind (und auch so klingen!)
Für einen Filtereffekt muß man mindestens zwei aufeinanderfolgende „Samplepunkte“ verrechnen. Dies sind der aktuelle Wert aus dem Oszillator und sein Vorgängerwert. Das arithmetische Mittel ((Wert1 + akueller Wert) dividiert durch 2) der beiden Punkte ist der nun neue aktuelle Wert. Da hiermit eine Spitzenbildung im Signalverlauf verringert wird und die Spitzen Obertöne im Spektrum repräsentieren, kommt das Ergebnis einer Reduktion der Obertöne, also einer Tiefpaßwirkung gleich!
Die dazugehörige Gleichung ist:
aktuellWert(Sample) = 0.5x(Sample) + 0.5x(VorherigesSample)
Einen Hochpaßeffekt kann man durch Subtraktion anstelle der Addition erreichen.
Eine allgemeine Gleichung mit variablem Durchlaßverhalten (in Form der Koeffizienten) sieht so aus. Achtung! („VorherigesSample“) entspricht dabei („Sample“-1):
aktuellWert(Sample) = ax(Sample) – bx(VorherigesSample)
Will man bestimmte Filter-Charakteristika besser bestimmen, braucht man die Betrachtung mehrerer Werte vor dem aktuellen Samplewert:
aktuellWert(Sample) = ax(Sample) + bx(Sample-1) +
cx(Sample-2) + etc..
Diesen Typ nennt man Finite Impulse Response (FIR), welcher noch keine Berücksichtigung der nun nötigen „Rückkopplung“ hat, eine mathematische Verbindung von Aus- zu Eingangswerten.
Der Infinite Impulse Response (IIR) genannte Filtertyp hat seinen Namen durch die unendliche („infinite“) Kette der Vorgängerwerte bekommen, während der FIR-Typ nur eine bestimmte „Stelle“ bearbeitet. Es wird der aktuelle Wert aus Anteilen der jeweils vorausgegangenen Werte ermittelt und verwertet:
1
_ x aktueller Samplewert addiert mit
2
1
_ x vorangehender Samplewert addiert mit
4
1
_ x Samplewert vor vorangehendem Samplewert addiert mit etc… –>
8
. .
. .
V V
Dieser Filtertyp (IIR) kann, wie oben erklärt, auch als Hochpaß fungieren, indem man die Brüche entsprechend subtrahiert (anstatt diese zu addieren). Von Vorteil ist also, möglichst viele Werte einzubeziehen („Rückkopplung“).
Die Nachteile sind in dieser Entwicklungsstufe: –
nichtlinearer Phasengang, –
aufwendige Rückkopplungsprogrammierung nötig-
hohe Auflösung (Wortbreite / Bitbreite)
wegen der Fehlereinberechnung nötig…-
keine Selbstoszillation…
Auch mit anderen Verfahren können Filter verwirklicht werden, wie etwa ein Kammfilter beispielsweise auch durch ein Delay (Verzögerung) mit Rückkopplung auf den Eingang erreicht werden kann. Auch Allpaßfilter können so generiert werden; hier spielen die Dämpfung der Rückkopplung und die Verknüpfung der Signale mit Multiplizierern und Addierern eine wichtige Rolle, dies findet in Korgs „Prophecy“ Solosynthesizer eine hörbare Lösung.
Auch Hall- und Echoeffekte (oder ähnlich diesen klingende Effekte) können mit Kamm- und Allpaßfilterkombinationen erzeugt werden, was für einen Synthesizer keine uninteressante Bereicherung darstellt. Viele Hersteller geben ihren Geräten bis zu achtfache Effektprozessoren (so auch die Korg „Trinity“) mit auf den Weg.
Für Aufgaben mit Rechnungen wie obige sind digitale Signal Prozessoren (DSP´s) sehr gut geeignet. In Clavias „Nord Lead“ ist ein DSP (aus der meistverwendeten „56000er-Familie“, hier ein 56002 FC40) für jeweils vier Stimmen zuständig. Zusammen mit einem Motorola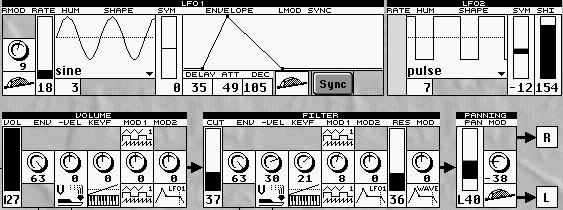 
MC68331(CFC16), einem Hauptprozessor mit der ungefähren Leistung eines Atari Falcon oder eines älteren Apple „68K Macintosh“ – Modells hat der Nord Lead mit drei DSPs zwölf Stimmen zur Verfügung. Der benötigte Platz für diese Hardware ist zudem äußerst gering! Wie im nächsten Kapitel näher erläutert, benutzt der Waldorf „Microwave 2“ eine sehr ähnliche Hardware!
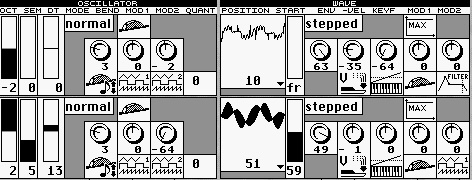
Die Oszillator-,Wave-, Misch- und LFO-Sektion des Microwave mit allen Modulationquellen.
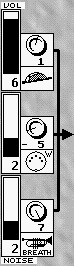
Mischer: Osc.Osc.2 Noise: rechts.
Die beiden LFO´s des WALDORF Microwave v.l.n.r.: LFO1,Minihüllkurve und LFO2
von l. nach r. : Lautstärke, Filter und Panorama – Einstellungen
